Lineare Funktionen sind ein grundlegendes Konzept in der Mathematik und spielen eine zentrale Rolle in vielen wissenschaftlichen und technischen Anwendungen. In diesem Artikel werden wir uns ansehen, was lineare Funktionen sind, wie sie dargestellt werden und wie sie in der Praxis verwendet werden können.
Was sind lineare Funktionen?
Eine lineare Funktion ist eine Funktion, die, wenn sie grafisch dargestellt wird, eine gerade Linie ergibt. Mathematisch ausgedrückt hat eine lineare Funktion die Form:
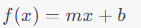
wobei m die Steigung der Linie und b der y-Achsenabschnitt ist.
- Steigung (m): Die Steigung gibt an, wie steil die Linie ist. Eine positive Steigung bedeutet, dass die Funktion mit zunehmendem x ansteigt, während eine negative Steigung bedeutet, dass die Funktion mit zunehmendem x abfällt.
- Y-Achsenabschnitt (b): Dies ist der Punkt, an dem die Linie die y-Achse schneidet. Es gibt den Wert von f(x) an, wenn x=0.
Eigenschaften
Lineare Funktionen haben folgende Eigenschaften:
- Ihr Graph ist eine Gerade.
- Die Steigung der Funktion gibt an, wie stark die y-Werte mit den x-Werten zunehmen.
- Der Achsenabschnitt gibt den y-Wert an, den die Funktion an der x-Achse annimmt.
Beispiele
Hier sind einige Beispiele für lineare Funktionen:
- Die Funktion
y = 2x + 1hat eine Steigung von 2 und einen Achsenabschnitt von 1. Ihr Graph ist eine Gerade, die durch den Punkt (0, 1) verläuft und mit einer Steigung von 2 nach oben steigt. - Die Funktion
y = 1/2 x - 1hat eine Steigung von 1/2 und einen Achsenabschnitt von -1. Ihr Graph ist eine Gerade, die durch den Punkt (0, -1) verläuft und mit einer Steigung von 1/2 nach rechts unten abfällt. - Die Funktion
y = 0hat eine Steigung von 0 und einen Achsenabschnitt von 0. Ihr Graph ist eine horizontale Gerade, die durch den Punkt (0, 0) verläuft.
Visualisierung
Lineare Funktionen lassen sich leicht mithilfe von Tabellen, Graphen und Diagrammen darstellen.
Tabellen
In einer Tabelle kann man die Werte einer linearen Funktion in der Form (x, y) angeben. Hier ist ein Beispiel für eine Tabelle, die die Funktion y = 2x + 1 darstellt:
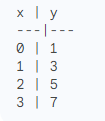
Graphen
Der Graph einer linearen Funktion ist eine Gerade. Die Steigung der Funktion kann man anhand des Graphen ermitteln, indem man zwei Punkte auf der Geraden markiert und den Winkel zwischen diesen beiden Punkten und der x-Achse bestimmt. Der Achsenabschnitt der Funktion ist der Schnittpunkt der Geraden mit der y-Achse.
Hier ist ein Beispiel für einen Graph der Funktion y = 2x + 1:
Diagramme
Ein Diagramm ist eine visuelle Darstellung von Daten, die in Form von Punkten dargestellt werden. Ein Diagramm kann verwendet werden, um die Beziehung zwischen zwei Variablen zu veranschaulichen.
Hier ist ein Beispiel für ein Diagramm, das die Beziehung zwischen der Temperatur und dem Zeitverlauf darstellt:
Anwendung
Lineare Funktionen werden in vielen Bereichen der Mathematik, der Naturwissenschaften und der Technik verwendet. Hier sind einige Beispiele:
- In der Physik werden lineare Funktionen verwendet, um die Bewegung von Objekten zu beschreiben.
- In der Chemie werden lineare Funktionen verwendet, um die Konzentration von Stoffen in einer Lösung zu beschreiben.
- In der Wirtschaft werden lineare Funktionen verwendet, um Kosten und Gewinne zu beschreiben.
- In der Technik werden lineare Funktionen verwendet, um die Funktionsweise von Maschinen zu beschreiben.
Lineare Funktionen sind ein wichtiges Werkzeug, um lineare Beziehungen zu verstehen und zu modellieren.

