Subscribe

Get my Updates
All Downloads List of All Posts

SPIELTHEORIE

Allgemeines

mehr Informationen zu diesen Open Yale course und die Downloadmöglichkeit dazu findet man unter [Econ 159]

Normalform

Ein Spiel in strategischer Form wir durch folgende Informationen beschrieben:

  • Menge der Spieler
  • Die Strategiemenge jedes Spielers (die möglichen Handlungsalternativen)
  • Die Auszahlung für die Spieler (als Funktion aller möglicher Handlungskombinationen)

Jedes strategische Spiel kann in einer Spielmatrix (Normalform) dargestellt werden.

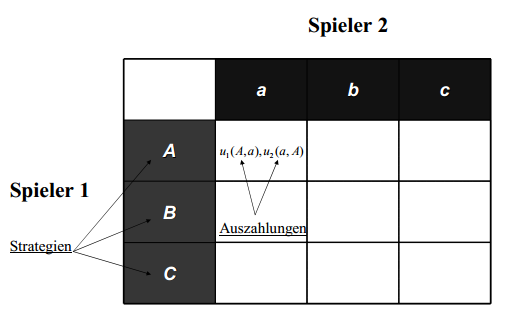
Der Spieler 1 hat die Handlungsalternativen A,B,C und der Spieler 2 hat die Handlungsalternativen a,b,c. Wählt der Spieler 1 die Handlungsalternative A und der Spieler B die Handlungsalternative b kommt es zu beispielsweise zu den Auszahlungen 5/-5 (u1(A,a),u2(a,A)).
Am Beispiel von Stein, Schere Papier, würde eine solche Normalform bei 2 Spielern folgendermaßen aussehen:

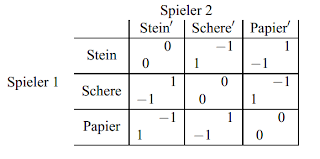
Beschreibung: Die Namen der Spieler werden oben über die Matrix und links daneben geschrieben. Die Handlungsalternativen / Strategien der beiden Spieler werden über die Spalten und vor die Zeilen geschrieben. Jede Zelle der Matrix beschreibt die Auszahlung bei einer Kombination von Handlungsalternativen. Die erste Zahl entspricht der Auszahlung, die der Spieler 1 bekommt und die zweite Zahl entspricht der Auszahlung, die der Spieler 2 bekommt.
Links:

Nash-Gleichgewicht

Definition: Das Nash-Gleichgewicht ist eine Strategienkombination, in der keiner der Spieler einen Anreiz hat, als Einziger von der Gleichgewichtskombination abzuweichen. Das Nash-Gleichgewicht ist damit eine Strategienkombination, die sich nicht aus sich selbst heraus zerstört, sondern zu gewissem Grad stabil ist – daher der Name Gleichgewicht. 

Unterscheidung der Spiele:

  • Bimatrixspiel (Zweipersonenspiel in Normalform)
  • Matrixspiel (symetrisches Spiel in Normalform)

Beispiele für Spiele mit Nash-Gleichgewichten

  • Gefangenendilemma
  • Koordinationsspiele
  • Battle of Sexes
  • Hawk-Dove / Chicken
  • Matching Pennies

Koordinationsspiele: Koordinationsspiele sind Spiele mit mehreren Nash-Gleichgewichten in reiner Strategie, bei denen beide Spieler dieselbe Strategie wählen müssen. Dh. die Spieler haben übereinstimmende Interessen.

Nullsummenspiele: Nullsummenspiele sind Spiele bei denen sich bei der Addition der Auszahlungen 0 herauskommt. Anders formiert, was der eine gewinnt, verliert der andere. 

gutes Beispiel: Zwei Autofahrer kommen sich auf einer Straße entgegen. Beide fahren auf derselben Straßenseite. Es gibt nun folgende Strategien: Jeder Fahrer kann entweder die Seite wechseln oder auf seiner Seite bleiben. Dabei soll unterstellt werden, dass beide Fahrer nur simultan handeln können. Wenn wir ein reibungsloses Passieren der beiden Autos mit 0 und einen Crash mit -100 für beide Fahrer bewerten, ergibt sich folgende Payoff-Matrix:

 Fahrer A/B     wechselt bleibt
wechselt-100/-1000/0 
bleibt 0/0 -100/-100 

Hier gibt es zwei Nash-Gleichgewichte in reinen Strategien, entweder beide weichen nach links aus oder beide nach rechts. Es spielt also keine Rolle, welche Seite sie wählen, solange sie nur beide dieselbe wählen. Beide Lösungen sind pareto-effizient.

Koordinationsspiel ohne Verteilungskonflikt

Koordinationsspiel mit Verteilungskonfilkt – Kampf der Geschlechter (battle of sexes)

Beim Kampf der Geschlechter geht es darum, dass zwei Personen einen gemeinsamen Abend verbringen möchten (zB Fußball, Konzert). Beide Personen müssen unabhängig voneinander entscheiden. Die Auszahlungsmatrix (Payoff-Matrix) würde folgendermaßen aussehen:

Mann/FrauFußballKonzert
Fußball3/10/0 
Konzert0/0 1/3 

Das Spiel hat 2 Nash-Gleichgewichte Mann:Fußball & Frau:Fußall sowie Mann:Konzert & Frau:Konzert. Das Problem dieses Spiels ist nun, dass es keine dominanten Strategien gibt. Wenn die beiden Spieler gleichzeitig ihre Lieblingsalternative (Frau geht ins Konzert, Mann zum Fußball.) wählen, kommt es zu keinem Treffen, was für beide nicht optimal ist. Sie würden in diesem Fall doch lieber an den Ort gehen, den der jeweils andere bevorzugt – Hauptsache, sie sind zusammen. Wenn aber beide so denken und dem anderen entgegenkommen möchten, treffen sie sich wieder nicht. 

reine Strategie vs. gemischte Strategie

In einem Spiel mit simultanen Zügen müssen die  Spieler ihre Handlungen ohne jede Kenntnis der Handlungen der anderen Spieler wählen. Spiele mit simultanen Zügen gliedern sich in:

  • Reine Strategie bedeutet, dass jeder Spiele seine Strategie eindeutig determiniert hat. Der Spieler legt sich auf eine Strategie fest und wendet diese wiederholt an. Dh. Es erfolgt eine Festlegung eines vollständigen Handlungsplans. 
  • Bei einer gemischten Strategie trifft der Spieler keine direkte Entscheidung, sondern er wählt einen Zufallsmechanismus, der eine reine Strategie bestimmt. dh. Es wird die Handlung zufällig gewählt (zB Stein-Schere-Papier, Elfmenter)

Links

noch einzuarbeiten:

Gefangenendilemma

Problemstellung: Zwei Gefangene werden verdächtigt, gemeinsam eine Straftat begangen zu haben. Beide Gefangene werden in getrennten Räumen verhört und haben keine Möglichkeit, sich zu beraten bzw. ihr Verhalten abzustimmen. Die Höchststrafe für das Verbrechen beträgt sechs Jahre. Wenn die Gefangenen sich entscheiden zu schweigen (Kooperation), werden beide wegen kleinerer Delikte zu je zwei Jahren Haft verurteilt. Gestehen jedoch beide die Tat (Defektion), erwartet beide eine Gefängnisstrafe, wegen der Zusammenarbeit mit den Ermittlungsbehörden jedoch nicht die Höchststrafe, sondern lediglich von vier Jahren. Gesteht nur einer (Defektion) und der andere schweigt (Kooperation), bekommt der erste als Kronzeuge eine symbolische einjährige Bewährungsstrafe und der andere bekommt die Höchststrafe von sechs Jahren.


optimale Strategie:Tit for Tat – Kooperiert in der ersten Runde und kopiert in den nächsten Runden den vorherigen Spielzug des Spielpartners. Diese Strategie ist prinzipiell kooperationswillig, übt aber bei Verrat Vergeltung. Bei erneuter Kooperation des Mitspielers ist sie nicht nachtragend, sondern reagiert ihrerseits mit Kooperation.

Wikipedia | Prisoner’s dilemma

weitere Spiele

Das Ultimatumspiel – Gefühl für Fairness oder Furcht vor Ablehnung (Ultimatum game)

Spielregeln: Ein Akteur, Spieler 1, macht zunächst ein Angebot über die Aufteilung eines vorgegebenen Geldbetrags, das Spieler 2 anschließend annehmen oder ablehnen kann. Akzeptiert er den Vorschlag von Spieler 1, so wird dieser umgesetzt und an die Spieler ausgezahlt. Lehnt er jedoch ab, so erhalten beide Spieler nichts.

Ziegenproblem / Monty-Hall-Problem

Problemstellung: „Nehmen Sie an, Sie wären in einer Spielshow und hätten die Wahl zwischen drei Toren. Hinter einem der Tore ist ein Auto, hinter den anderen sind Ziegen. Sie wählen ein Tor, sagen wir, Tor Nummer 1, und der Showmaster, der weiß, was hinter den Toren ist, öffnet ein anderes Tor, sagen wir, Nummer 3, hinter dem eine Ziege steht. Er fragt Sie nun: ,Möchten Sie das Tor Nummer 2?‘ Ist es von Vorteil, die Wahl des Tores zu ändern?

Am einfachsten lässt es sich mit einem Baumdiagramm erklären, in dem alle möglichen Ausgänge und ihre Wahrscheinlichkeiten eingezeichnet sind. 

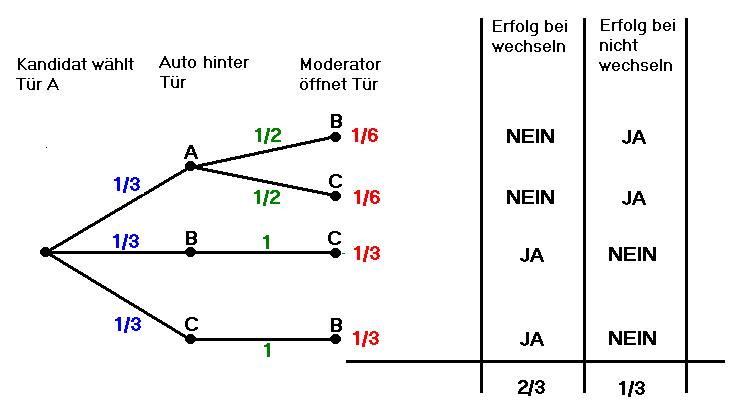
Quelle: hier

Literatur

deutschsprachige Literatur

englischsprachige Literatur

  • Fudenberg, Drew – Game Theory
  • Osborne, Martin J. – A Couse in Game Theory
  • Osborne, MartinJ. – Bargaining and Markets
  • Davis, Morton – Game Theory (A Nontechnical introduction)
  • von Neumann, John – Theory of Games and Economic Behaviour

Wer zum Lesen zu faul ist, und gut Englisch kann, dem kann ich Games People Play: Game Theory in Life, Business and Beyond DVD Teaching Company Great Courses (The Great Courses Business & Economics, 1 & 2) empfehlen.

Downloads

Cookie Consent Banner von Real Cookie Banner