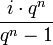Einführung
Tilgungsrechnung ist ein zentraler Bestandteil der Finanzmathematik und befasst sich mit der systematischen Rückzahlung von Schulden oder Darlehen. Wenn ein Kreditnehmer Geld von einem Kreditgeber leiht, muss dieser Betrag über einen festgelegten Zeitraum zurückgezahlt werden, oft zuzüglich Zinsen. Die Tilgungsrechnung legt fest, wie und in welchen Raten dieser geliehene Betrag zurückgezahlt wird, sodass am Ende der vereinbarten Laufzeit die Schuld vollständig beglichen ist.
Annuitätentilgung
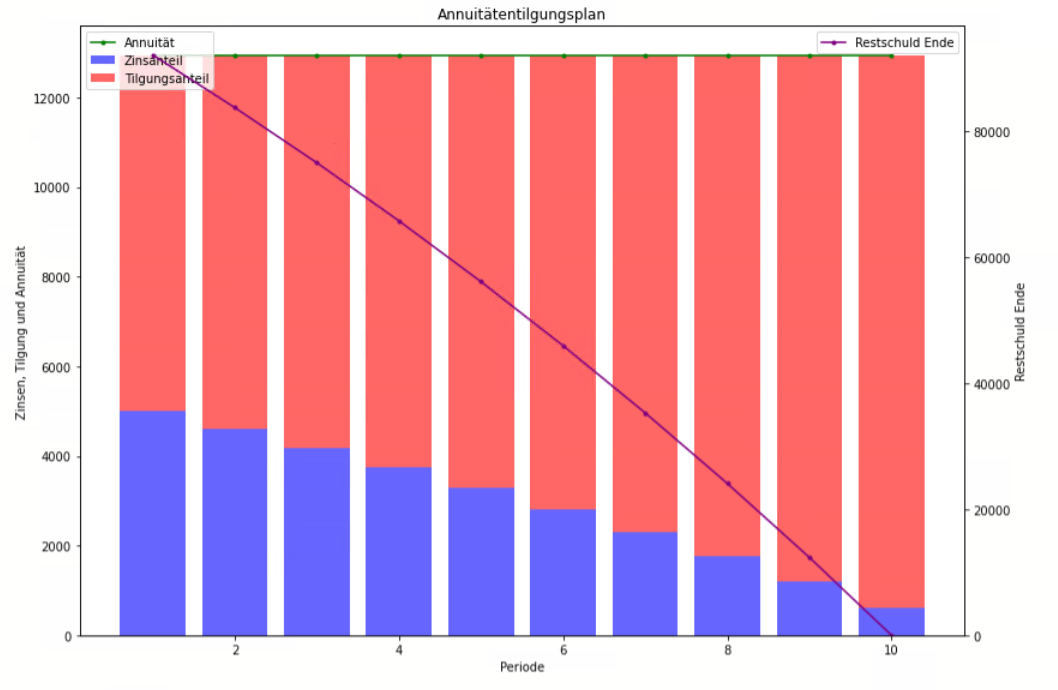
Bei der Annuitätentilgung bleiben die jährlichen Raten, auch Annuitäten genannt, über die gesamte Laufzeit hinweg konstant. Diese Rate setzt sich aus einem Zins- und einem Tilgungsanteil zusammen. Während der Zinsanteil über die Laufzeit hinweg abnimmt, steigt der Tilgungsanteil entsprechend an, sodass die Gesamtrate gleichbleibend ist.
= die Rückzahlungen/Kapitaldienst/Annuitäten sind konstantnicht konstant:
- (Tilgungs-)Raten (steigt)
- Zinskomponente (fällt)
Formel
Berechnung der Annuität
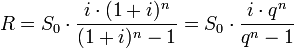
wobei folgendes der Annuitätenfaktor ist:
mit anderen Worten:
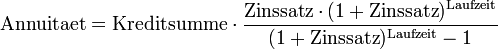
Berechnung der Restschuld, Zinsen, Tilgung in einem beliebigen Jahr:
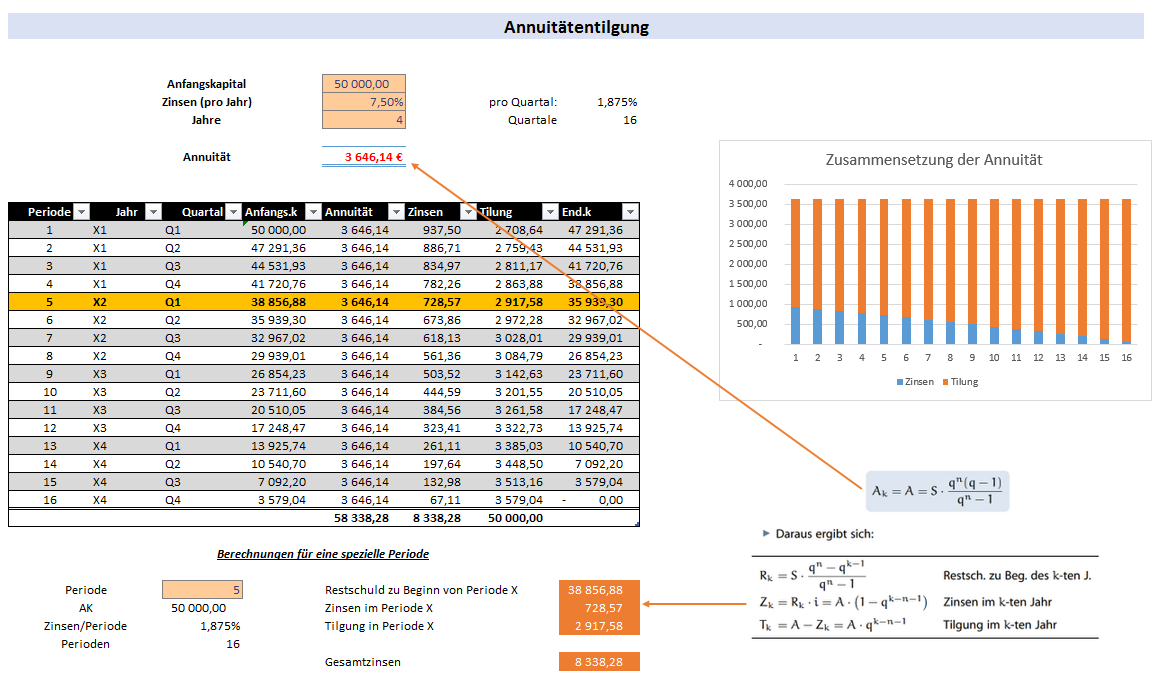
Excel
In Excel gibt es die Funkion RMZ [Rgelmäßige Zahlung] um die konstante Rückzahlung (Annuität zu berechnen)= RMZ(Zins;Zzr;Bw;Zw;F)Excel - RMZhttps://www.youtube.com/embed/HpDTIBVl398?rel=0&wmode=opaqueschwieriger wird es, wenn man für eine bestimmte Periode die Restschuld … errechnen möchte, ohne einen Tilgungsplan aufzustellen. Dann kann man die in der oben gezeigten Excel-Tabelle verwendeten Formeln benutzen.
| Restschuld zu Beginn von Periode X | =AK*((1+Zins)^PeriodenGesamt-(1+Zins)^(PeriodeX-1))/((1+Zins)^PeriodenGesamt-1) |
| Zinsen in Periode X | =ABS(RMZ(Zins;PeriodenGesamt;AK))*(1-(1+Zins)^(PeriodeX-PeriodenGesamt-1)) |
| Tilgung in Periode X | =ABS(RMZ(Zins;PeriodenGesamt;AK))*(1+Zins)^(PeriodeX-PeriodenGesamt-1) |
Da das schwer zu merken ist hier die VBA-Funktionen dazu:
Public Function AnnTilg_TilgungPeriodeX(Zins As Double, PeriodenGesamt As Integer, AK As Double, PeriodeX As Integer) As Double AnnTilg_TilgungPeriodeX = Application.Evaluate("=ABS(PMT(Zins,PeriodenGesamt,AK))*(1+Zins)^(PeriodeX-PeriodenGesamt-1)") End Function Public Function AnnTilg_RestSchuldBeginnPeriodeX(Zins As Double, PeriodenGesamt As Integer, AK As Double, PeriodeX As Integer) As Double AnnTilg_RestSchuldBeginnPeriodeX = Application.Evaluate("=AK*((1+Zins)^PeriodenGesamt-(1+Zins)^(PeriodeX-1))/((1+Zins)^PeriodenGesamt-1)") End Function Public Function AnnTilg_ZinsenPeriodeX(Zins As Double, PeriodenGesamt As Integer, AK As Double, PeriodeX As Integer) As Double AnnTilg_ZinsenPeriodeX = Application.Evaluate("=ABS(PMT(Zins,PeriodenGesamt,AK))*(1-(1+Zins)^(PeriodeX-PeriodenGesamt-1))") End Function Public Function AnnTilg_GesamtZinsen(Zins As Double, PeriodenGesamt As Integer, AK As Double) As Double Dim sTerm As String sTerm = "=ABS(PMT(Zins;PeriodenGesamt;AK))*(1-(1+Zins)^(x-PeriodenGesamt-1))" sTerm = Replace(sTerm, "Zins", Zins) sTerm = Replace(sTerm, "PeriodenGesamt", PeriodenGesamt) sTerm = Replace(sTerm, "AK", AK) Dim i As Integer sTerm = Replace(sTerm, ",", ".") 'Komma berichtigen sTerm = Replace(sTerm, ";", ",") 'Trennzeichen in Formeln berichtigen For i = 1 To PeriodenGesamt AnnTilg_GesamtZinsen = AnnTilg_GesamtZinsen + Application.Evaluate(Replace(sTerm, "x", i)) Next End Function
Download
Links
- Annuitätentilgung (Wikipedia)
- Vor- und Nachteils von Annuitätendarlehn
- Annuitätentilgung mit einigen Beispielen
- Noch ein Geheimnis des Annuitätendarlehens: Die Zinsanomalie,oder wenn weniger mehr ist
- Reuse, Svend – Anleitung zum Erstellen eines Excel-Sheets für die Berechnung eines Annuitätendarlehns
Ratentilgung (lineare Tilgung)
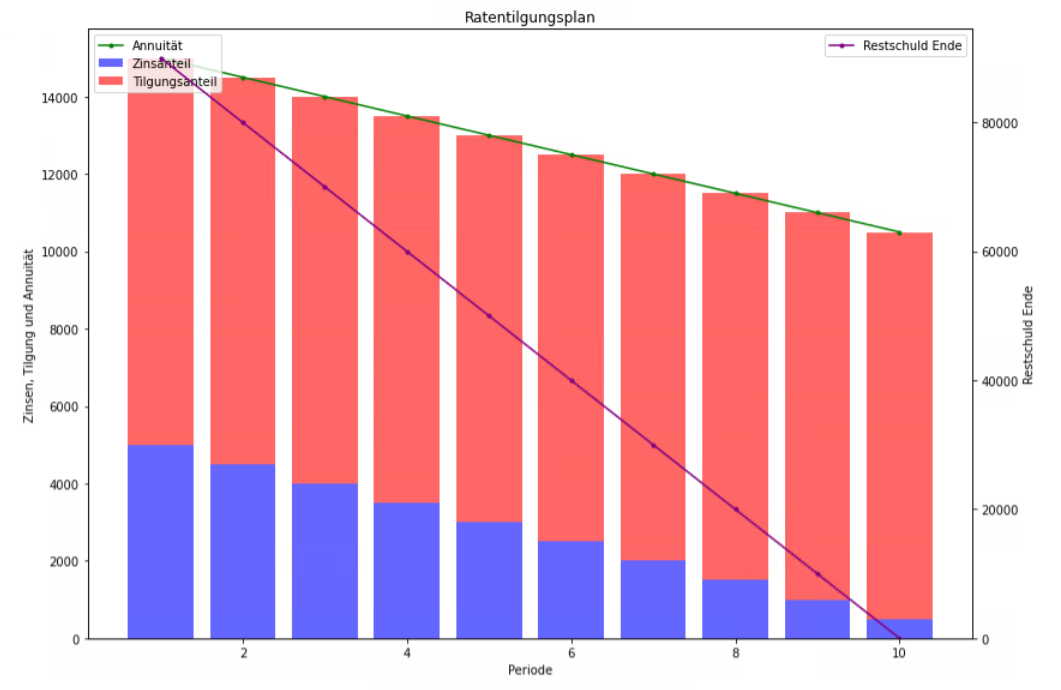
Bei dieser Art der Tilgung bleibt der Tilgungsanteil über die gesamte Laufzeit konstant. Das bedeutet, dass der Kreditnehmer jedes Jahr denselben Betrag zur Tilgung des Darlehens leistet. Der Zinsanteil verringert sich jedoch jedes Jahr, da die Restschuld sinkt. Dadurch verringert sich die Gesamtrate von Jahr zu Jahr.
= die (Tilgungs-)Raten sind konstant nicht konstant:
- Annuität (fallend)
- Zinsaufwand (Zinskomponente) (fallend)
- Tilgungsanteil (konstant)
Die monatliche Rate R eines Darlehns mit einer anfänglichen Darlehnssumme D, einem jährlichen Zinssatz z und einer Laufzeit von n Jahren (mit monatlicher Tilgung) kann mit folgender Formel berechnet werden.
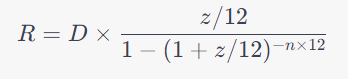
Für die jährliche Tilgung ergibt sich folgende Formel:
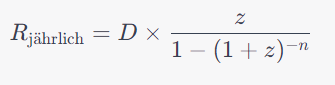
endfällige Tilgung (Bullet-Darlehn)
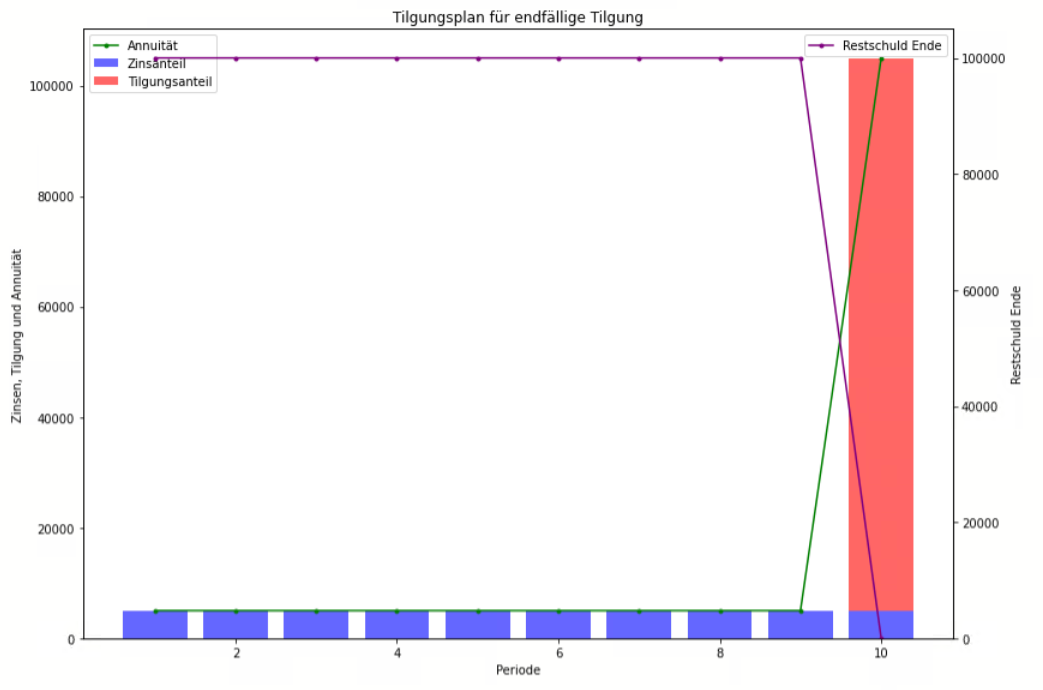
Bei der endfälligen Tilgung werden während der Laufzeit nur die Zinsen des Darlehens gezahlt. Die gesamte Kreditsumme wird dann am Ende der Laufzeit in einer einzigen Rate zurückgezahlt. Diese Art der Tilgung ist besonders bei bestimmten Investitionsformen, wie z.B. bei einigen Bausparverträgen, üblich.
Die Formel zur Berechnung des jährlichen Zinsbetrags bei der endfälligen Tilgung ist:
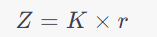
wobei:
- Z der jährliche Zinsbetrag ist
- K der Kreditbetrag ist
- r der jährliche Zinssatz ist
Tilgungsfreie Zeiten
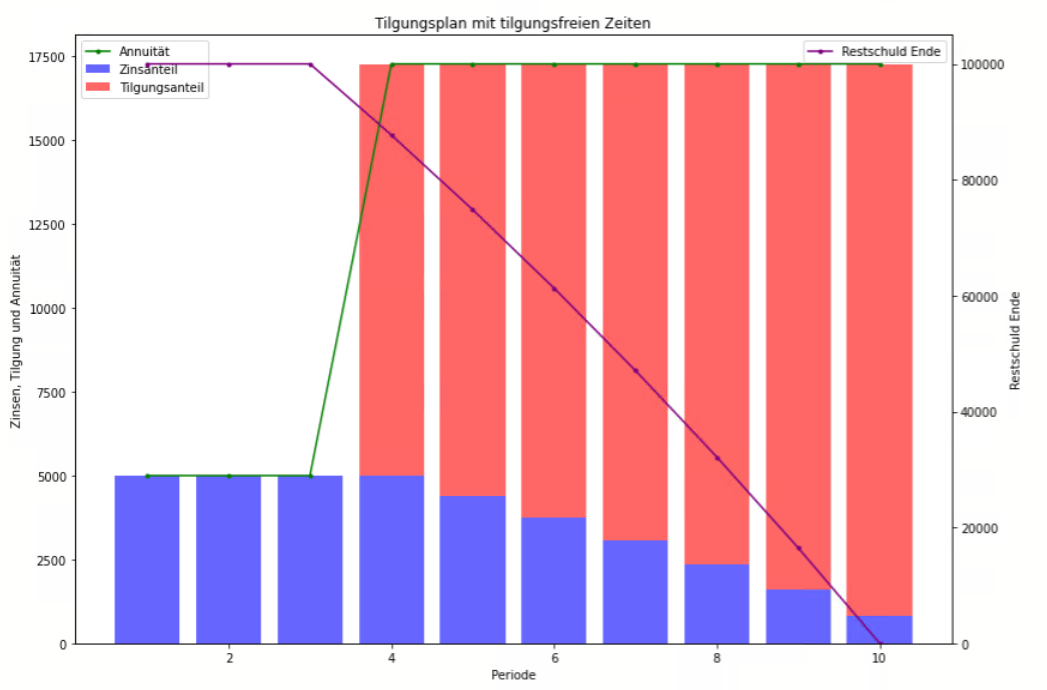
Hierbei handelt es sich um Darlehensverträge, bei denen für einen bestimmten Zeitraum zu Beginn des Darlehens keine Tilgung geleistet wird. Während dieser Phase werden nur die Zinsen gezahlt. Nach Ablauf der tilgungsfreien Zeit beginnt die reguläre Tilgung des Darlehens.
Die jährliche Zinszahlung während der tilgungsfreien Jahre beträgt:
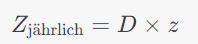
Nach Ablauf der tilgungsfreien Jahre (m) berechnet sich die jährliche Rate für die verbleibende Laufzeit (n-m). Die jährliche Rate R(jährlich) kann mit folgender Formel berechnet werden:
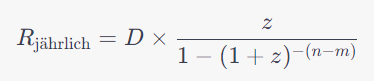
Tilgung mit benuzterdefinierten Perioden
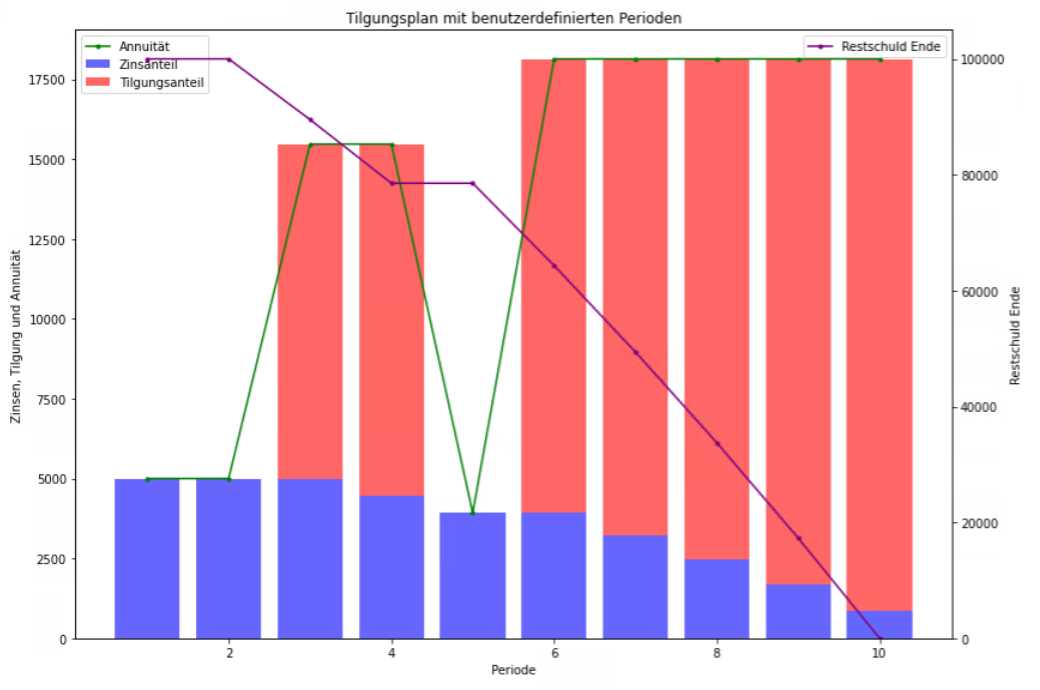
Eine Tilgung mit benutzerdefinierten Perioden erlaubt es, die Tilgungsstruktur eines Darlehens flexibel zu gestalten. Anstatt einer festen Regel, wie z.B. “die ersten x Jahre sind tilgungsfrei”, können Sie genau festlegen, welche Perioden (z.B. Jahre oder Monate) tilgungsfrei sind und welche nicht. Das bietet eine größere Anpassungsfähigkeit an individuelle finanzielle Situationen oder Geschäftsanforderungen.
Wenn Sie beispielsweise angeben, dass die Perioden 1, 2 und 5 tilgungsfrei sind, bedeutet das:
- In den Perioden 1, 2 und 5 zahlen Sie nur die Zinsen auf die verbleibende Darlehenssumme, und die Hauptsumme des Darlehens bleibt unverändert.
- In allen anderen Perioden zahlen Sie sowohl Zinsen als auch Tilgung, wodurch sich die Darlehenssumme reduziert.
Variable Tilgung
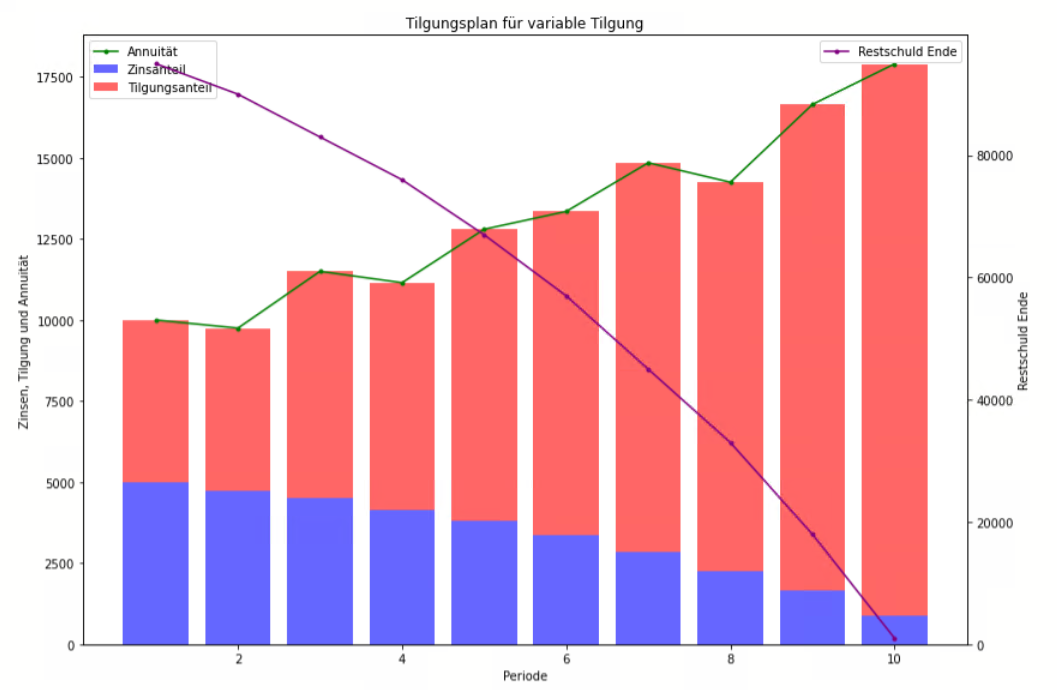
Bei dieser Tilgungsart hat der Kreditnehmer die Möglichkeit, die Höhe der Tilgungsraten während der Laufzeit anzupassen. Dies kann beispielsweise in Abhängigkeit von der aktuellen finanziellen Situation des Kreditnehmers geschehen.
Tilgungsdarlehn
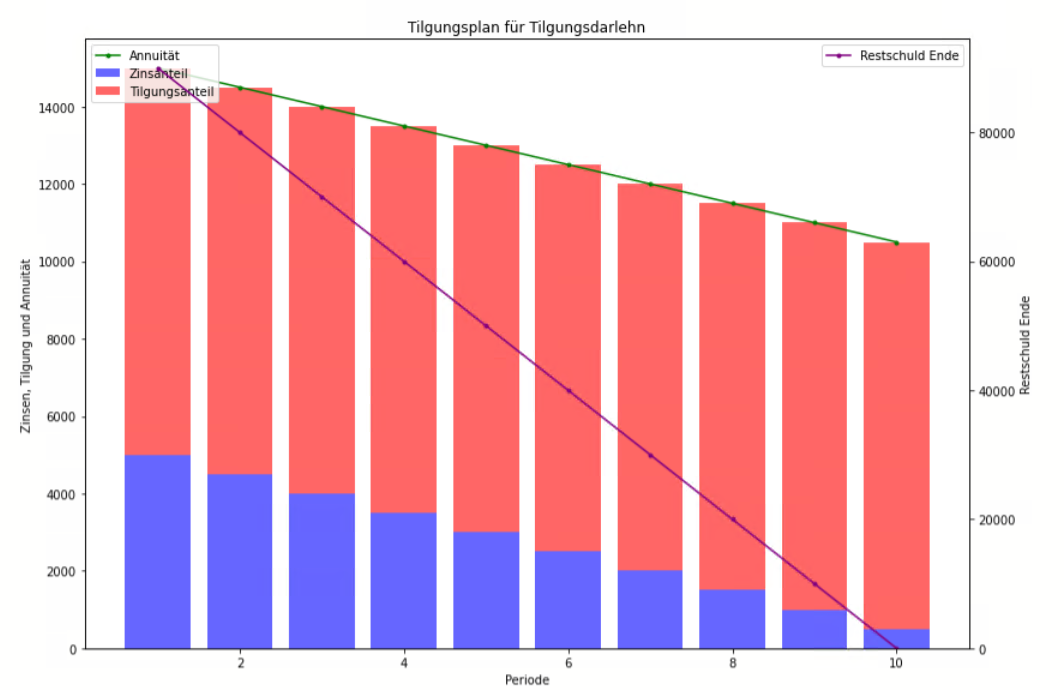
Ein fester Betrag wird regelmäßig getilgt, beispielsweise monatlich oder jährlich. Die Zinsen werden dabei nur auf den noch ausstehenden Betrag berechnet, wodurch sich der Zinsanteil kontinuierlich verringert.
Tilgungsrechnung in Python
Fazit
Die Wahl der passenden Tilgungsart hängt von verschiedenen Faktoren ab, einschließlich der finanziellen Situation des Kreditnehmers, der Laufzeit des Darlehens und den spezifischen Anforderungen und Zielen des Kreditnehmers. Es ist wichtig, die verschiedenen Optionen zu verstehen und sorgfältig abzuwägen, um eine fundierte Entscheidung über die Rückzahlungsstrategie eines Darlehens zu treffen.