Verteilungen
Es gibt viele verschiedene Arten von Verteilungen in der Statistik, hier sind einige der wichtigsten:
- Normalverteilung: Die Normalverteilung ist eine symmetrische Verteilung, die häufig als “Glockenkurve” dargestellt wird. Sie wird oft verwendet, um zufällige Messwerte oder Fehlerterme zu modellieren.
- Binomialverteilung: Die Binomialverteilung beschreibt die Verteilung von Erfolgswahrscheinlichkeiten bei wiederholten Bernoulli-Experimenten, bei denen nur zwei Ergebnisse möglich sind (z.B. Erfolg oder Misserfolg).
- Poisson-Verteilung: Die Poisson-Verteilung beschreibt die Verteilung von Ereignissen, die unabhängig voneinander in einem gegebenen Zeitintervall auftreten (z.B. Kunden, die einen Supermarkt betreten).
- Exponentialverteilung: Die Exponentialverteilung beschreibt die Verteilung von Wartezeiten zwischen unabhängigen Ereignissen (z.B. Kunden, die eine Bankfiliale betreten).
- Weibull-Verteilung: Die Weibull-Verteilung wird häufig verwendet, um die Lebenserwartung von Produkten oder die Wahrscheinlichkeit von Ereignissen zu modellieren, die sich im Laufe der Zeit verändern (z.B. das Risiko von Maschinenausfällen).
- Die Gamma-Verteilung ist eine Verteilung von positiven reellen Werten und wird häufig verwendet, um zufällige Zeitintervalle zu modellieren (z.B. die Dauer von Maschinenausfällen oder die Dauer von Kundenbesuchen).
- Chi-Quadrat-Verteilung: Die Chi-Quadrat-Verteilung wird verwendet, um die Summe der Quadrate von normalverteilten Zufallsvariablen zu modellieren und wird häufig in Tests von Hypothesen und in der Varianzanalyse verwendet.
- Student-t-Verteilung: Die Student-t-Verteilung wird verwendet, um die Abweichung von Schätzwerten von den tatsächlichen Werten zu modellieren, insbesondere in Fällen, in denen die Stichprobe klein ist oder die Populationsvarianz unbekannt ist.
- F-Verteilung (Fisher-Verteilung): Die F-Verteilung wird verwendet, um den Unterschied zwischen zwei Varianzen zu testen und wird häufig in der Varianzanalyse verwendet.
- Hypergeometrische Verteilung: Die Hypergeometrische Verteilung beschreibt die Verteilung von Erfolgen in wiederholten Bernoulli-Experimenten, bei denen eine begrenzte Anzahl von Erfolgen und Misserfolgen möglich ist (z.B. die Auswahl von Kugeln aus einem Sack, wobei ein Teil der Kugeln rot und der andere Teil blau ist).
- Laplace-Verteilung: Die Laplace-Verteilung, auch als Doppelt-Exponentialverteilung bekannt, wird häufig verwendet, um zufällige Fehlerterme oder Abweichungen von Schätzwerten zu modellieren. Sie hat eine symmetrische, zweimodale Verteilung, die sich gut für die Modellierung von Daten eignet, die “outliers” oder außergewöhnliche Werte enthalten.
- Log-Normal-Verteilung: Die Log-Normal-Verteilung wird verwendet, um zufällige Größen zu modellieren, die positiv sind und deren Logarithmen normalverteilt sind. Sie wird häufig verwendet, um zufällige Größen zu modellieren, die sich exponentiell verändern, wie zum Beispiel die Größe von Partikeln oder die Lebenserwartung von Produkten.
- Pareto-Verteilung: Die Pareto-Verteilung wird verwendet, um zufällige Größen zu modellieren, die positiv sind und deren Werte im Allgemeinen größer als ein Schwellenwert sind. Sie wird häufig verwendet, um die Verteilung von Ressourcen oder Vermögenswerten zu modellieren, die eine ungleichmäßige Verteilung aufweisen.
Die Wahl der richtigen Verteilung hängt von der Art der Daten und dem Zweck der Analyse ab. In einigen Fällen kann es erforderlich sein, mehrere Verteilungen zu vergleichen, um die beste Passform für die Daten zu finden. Es ist auch wichtig zu beachten, dass viele Verteilungen Annahmen über die Daten treffen, die möglicherweise nicht immer erfüllt sind. In solchen Fällen können alternative Verteilungen oder Anpassungsmethoden verwendet werden, um die Genauigkeit der Analysen zu verbessern.
Begriffe
empirische Momente
Die empirischen Momente einer Stichprobe sind Statistiken, die die Stichprobe beschreiben und Aufschluss über die Verteilung der Stichprobe geben. Es gibt verschiedene empirische Momente, die für verschiedene Zwecke verwendet werden können.
Das erste empirische Moment, das arithmetische Mittel, gibt den durchschnittlichen Wert der Stichprobe an. Es wird berechnet, indem man alle Werte der Stichprobe addiert und durch die Anzahl der Werte teilt.
Das zweite empirische Moment, die Varianz, gibt an, wie stark sich die Werte der Stichprobe um das arithmetische Mittel streuen. Es wird berechnet, indem man den Quadratischen Abstand jedes Werts zum arithmetischen Mittel berechnet, diese Quadratischen Abstände addiert und durch die Anzahl der Werte teilt. Die Standardabweichung ist die Wurzel aus der Varianz und gibt den mittleren Quadratischen Abstand der Werte zum arithmetischen Mittel an.
Das dritte empirische Moment, das Skewness-Koeffizient, gibt an, ob die Verteilung der Stichprobe symmetrisch oder asymmetrisch ist. Ein Skewness-Koeffizient von 0 bedeutet, dass die Verteilung symmetrisch ist, während ein Skewness-Koeffizient größer als 0 bedeutet, dass die Verteilung rechtsschief ist und ein Skewness-Koeffizient kleiner als 0 bedeutet, dass die Verteilung linksschief ist.
Das vierte empirische Moment, der Kurtosis-Koeffizient, gibt an, wie wölbt oder platt die Verteilung der Stichprobe ist. Ein Kurtosis-Koeffizient von 0 bedeutet, dass die Verteilung eine gleiche Wölbung wie die Normalverteilung hat. Ein Kurtosis-Koeffizient größer als 0 bedeutet, dass die Verteilung schärfer oder spitzer als die Normalverteilung ist, während ein Kurtosis-Koeffizient kleiner als 0 bedeutet, dass die Verteilung flacher als die Normalverteilung ist.
Die empirischen Momente sind wichtige Statistiken, die verwendet werden, um die Eigenschaften von Stichproben zu beschreiben und Vorhersagen über die Verteilungen von Populationswerten zu treffen. Sie werden häufig in der Statistik und im Maschinellen Lernen verwendet.
Skewness-Koeffizient
Der Skewness-Koeffizient ist ein Maß für die Schiefe einer Verteilung. Er gibt an, ob die Verteilung rechtsschief, linksschief oder symmetrisch ist.
Eine Verteilung ist rechtsschief, wenn der lange Schwanz der Verteilung nach rechts zeigt, das heißt, wenn es mehr extreme Werte in der rechten Hälfte der Verteilung gibt. Eine Verteilung ist linksschief, wenn der lange Schwanz der Verteilung nach links zeigt, das heißt, wenn es mehr extreme Werte in der linken Hälfte der Verteilung gibt. Eine Verteilung ist symmetrisch, wenn sie genau in der Mitte gespiegelt werden kann, das heißt, wenn der linke und der rechte Teil der Verteilung gleich aussehen.
Der Skewness-Koeffizient wird verwendet, um die Schiefe einer Verteilung zu messen und zu beschreiben. Er ist ein wichtiger Statistiker, der in der Statistik und im Maschinellen Lernen verwendet wird, um die Eigenschaften von Verteilungen zu beschreiben und Vorhersagen über deren Werte zu treffen.
Wölbung / Excess / Kurtosis
Die Wölbung einer Verteilung beschreibt die Form der Verteilung und gibt an, wie stark die Verteilung von den durchschnittlichen Werten abweicht. Eine Verteilung kann symmetrisch oder asymmetrisch sein und kann eine leicht positive, leicht negative oder keine Wölbung aufweisen.
Eine Verteilung ist symmetrisch, wenn sie genau in der Mitte gespiegelt werden kann, das heißt, wenn der linke und der rechte Teil der Verteilung gleich aussehen. Eine symmetrische Verteilung hat keine Wölbung. Ein Beispiel für eine symmetrische Verteilung ist die Normalverteilung.
Eine Verteilung ist asymmetrisch, wenn sie nicht in der Mitte gespiegelt werden kann, das heißt, wenn der linke und der rechte Teil der Verteilung unterschiedlich aussehen. Eine asymmetrische Verteilung kann entweder eine leicht positive oder eine leicht negative Wölbung aufweisen. Ein Beispiel für eine asymmetrische Verteilung mit leicht positivem Schwerpunkt ist die rechtsschiefe Verteilung. Ein Beispiel für eine asymmetrische Verteilung mit leicht negativem Schwerpunkt ist die linksschiefe Verteilung.
Die Wölbung einer Verteilung kann mit Hilfe von Statistiken wie dem Skewness-Koeffizienten oder dem Kurtosis-Koeffizienten gemessen werden. Die Wölbung einer Verteilung ist wichtig, da sie die Eigenschaften der Verteilung beschreibt und Auswirkungen auf Schätzungen und Vorhersagen hat, die auf den Daten basieren.
Berechnung: Als Maß für den Grad der Flach- oder Steilgipfligkeit kannst Du die Wölbung Deiner empirischen Verteilung als das vierte empirische Moment berechnen:
Da die Größe aus vierten Potenzen besteht, ist ihr Wert immer positiv; je geringer die Wölbung ist, umso flachgipfliger ist Deine Verteilung.
Exzess: Als Grenze zwischen flachgipfliger und steilgipfliger Verteilung wird das Wölbungsmaß der Normalverteilung gesetzt, das übrigens einen Wert von 3 aufweist. Deshalb wählt man für die Beurteilung einer Verteilung oft anstelle der Wölbung den Exzess, der sich durch Subtrahieren von 3 vom Wert der Wölbung ergibt:
Anhand des Exzesses einer Verteilung kannst Du die Einteilung dann noch einfacher anhand des Vorzeichens vornehmen, wie Entscheidungsregeln der Tabelle aufzeigen.

Normalverteilung
Beispiele für die Anwendung der Normalverteilung:
- Die Höhe von Menschen in einer Bevölkerung kann normalverteilt sein, mit einem Durchschnittswert von etwa 175 cm und einer Standardabweichung von etwa 7 cm. Das bedeutet, dass die meisten Menschen in der Bevölkerung eine Höhe von 175 cm +/- 14 cm (2 Standardabweichungen) haben.
- Die Qualität von Fertigungsteilen in einer Fabrik kann normalverteilt sein, mit einem Durchschnittswert von 100 und einer Standardabweichung von 5. Das bedeutet, dass die meisten Teile in der Fabrik eine Qualität von 100 +/- 10 (2 Standardabweichungen) haben.
- Die Intelligenzquotienten (IQ) von Menschen in einer Bevölkerung können normalverteilt sein, mit einem Durchschnittswert von 100 und einer Standardabweichung von 15. Das bedeutet, dass die meisten Menschen in der Bevölkerung einen IQ von 100 +/- 30 (2 Standardabweichungen) haben.
- Die Temperatur in einer Stadt im Sommer kann normalverteilt sein, mit einem Durchschnittswert von 30°C und einer Standardabweichung von 5°C. Das bedeutet, dass die meisten Tage in der Stadt eine Temperatur von 30°C +/- 10°C (2 Standardabweichungen) haben.
- Die Länge von Flussabschnitten kann normalverteilt sein, mit einem Durchschnittswert von 100 km und einer Standardabweichung von 20 km. Das bedeutet, dass die meisten Flussabschnitte eine Länge von 100 km +/- 40 km (2 Standardabweichungen) haben.
Jarque-Bera-Test
Der Jarque-Bera-Test ist ein statistischer Test, der anhand der Kurtosis und der Schiefe in den Daten prüft, ob eine Normalverteilung vorliegt.
Die Teststatistik JB des Jarque-Bera-Test ist definiert als
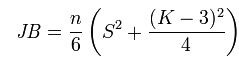
Wobei, unter
- S – die Schiefe gemeint ist
- K – die Kurtosis
Da K-3 den Exzess widerspiegelt, könnte man gleich in der obigen Formel den Exzess verwenden.
Links:

