Einführung
Als lineares Gleichungssystem bezeichnet man in der linearen Algebra ein System linearer Gleichungen, die mehrere unbekannte Größen (Variable) enthalten.
Ein entsprechendes System für drei Unbekannte sieht beispielsweise wie folgt aus:
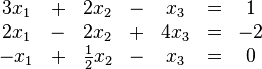
Allgemein lässt sich ein lineares Gleichungssystem mit m Gleichungen und n Unbekannten immer in die folgende Form bringen:
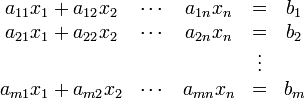
Für die Lösung derartiger Gleichungssysteme in Excel bringt man das lineare Gleichungssystem in eine sogenannte Koeffizientenmatrix:
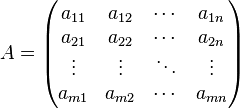
Es gibt in Excel mehrere Methoden, lineare Gleichungssysteme zu lösen:
- mittels Solver
- mittels Koeffizientenmatrix
Lösen lineare Gleichungssysteme in Excel als Matrix
Eine der Möglichkeiten in Excel Gleichungssysteme zu lösen stellt der Solver dar. Dabei werden die unterschiedlichen Variablen solange iteriert (durchprobiert) bis die gewünschten Kriterien erfüllt werden. Neben der Berechnung über Matrizen stellt die Lösungsmöglichkeit über den Solver die bekannteste Möglichkeit dar, Gleichungssysteme mit zwei oder mehr Variablen in Excel zu lösen.
Beispiel 1: lineares Gleichungssystem
Ausgangspunkt sind zwei Gleichungen (bzw. mehr Gleichungen) [der Vereinfachung der Erklärung werde ich vorerst nur ein Beispiel mit 2 Variablen verwenden]
- x+6=8*(y+6)
- x+13=4*(y+13)
Der Einfachheit halber werden die Gleichungen umgeformt (es ginge auch ohne Umformung, erfordert aber bei der Verwendung des Solvers größere Konzentration). Die umgeformten Gleichungen haben die Form:
- x-8y=42 (Umformung siehe Anhang)
- x-4y=39 (Umformung siehe Anhang)
Diese Ausgangsgleichungen bringt man nun in eine entsprechende Form. Man schreibt dazu die Koeffizienten x,y in eine Zeile und darunter die Anzahl der Auftreten dieser Koeffizienten. Für die erste Gleichung bedeutet das
- 1*x+-8*y = 42
- 1*x+-4*y = 39
Nun kann man für x und y beispielsweise 1 einsetzen und erhält folgendes Ergebnis:
- 1*1+-8*1=-7
- 1*1+-4*1=-3
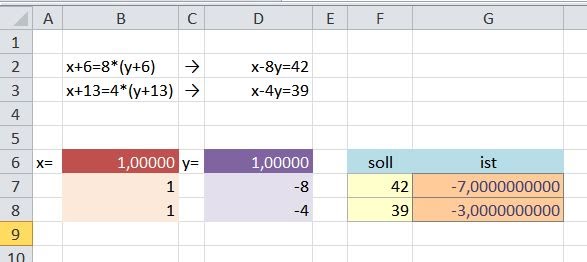
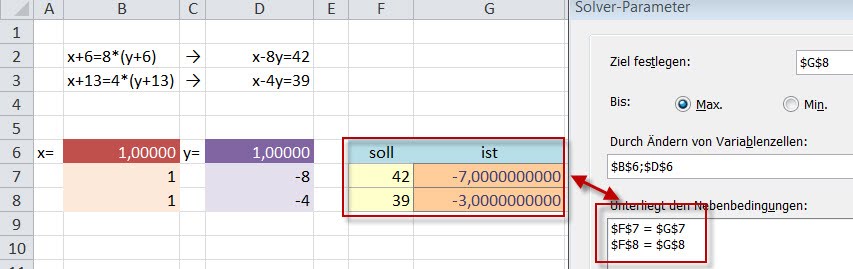
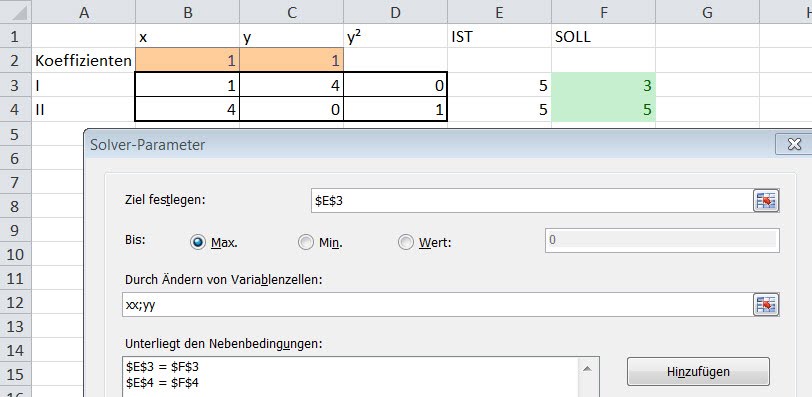
Nun beauftragt man den Solver alle Kombinationen von x und y durchzuprobieren, damit die Gleichungen den Soll-Werten entsprechen. Dafür findet man (sofern das Solver-Add-in aktiviert und installiert ist) im Reiter Daten den Solver.
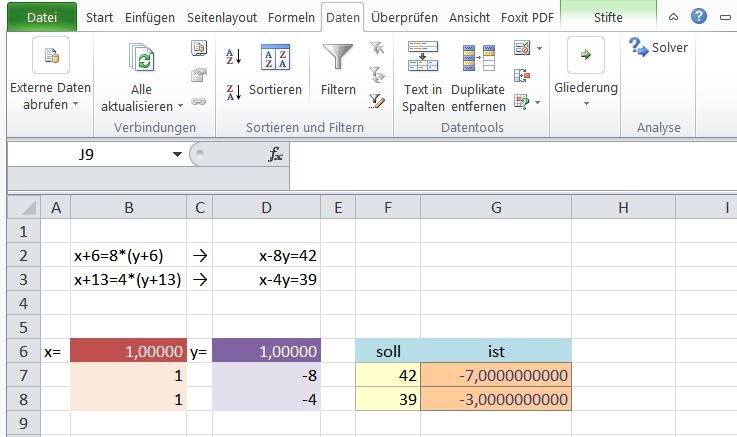
Nun müssen für den Solver die Kriterien eingegeben werden:
- Einerseits muss man ein Ziel festlegen. Dafür kann man den Ist-Wert jeder Gleichung festlegen. Der IST-Wert soll dem SOLL-Wert entsprechen:
- G7 = 42 oder
- G8 = 39
- Legt man dies alleine Fest, wird eine Lösung für x und y für die einzelne Gleichung ermittelt. Es muss daher eine Verbindung zwischen den beiden Gleichungen hergestellt werden. Dazu legt man als Nebenbedingung fest, dass auch für die zweite Gleichung der IST-Wert dem SOLL-Wert entsprechen muss. (Man kann auch wie im unteren Screenshot für beide SOLL-Werten festlegen, dass sie den IST-Werten entsprechen müssen)
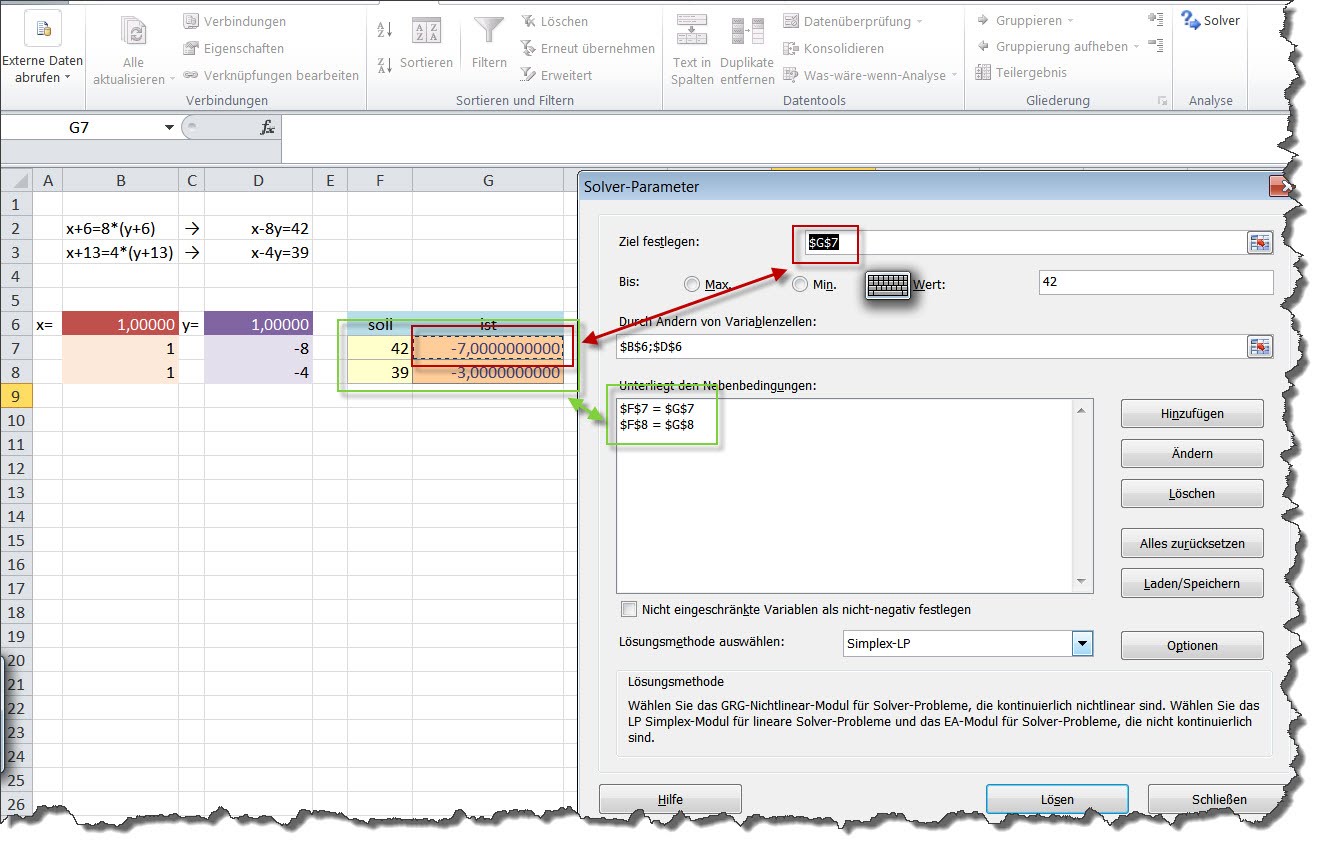
Die oben angeführten Kriterien können auf folgende Varianten im Solver eingegeben werden:
- Möglichkeit 1: Man probiert alle Werte durch, bis die erste Gleichung dem SOLL-WERT entspricht unter der Nebenbedingung, dass bei der zweiten Gleichung der IST-Wert dem SOLL-Wert entspricht.
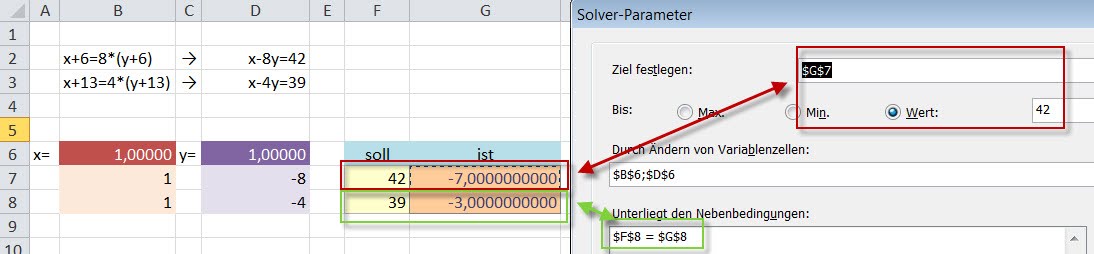
- Möglichkeit 2: Alternativ probiert man alle Werte durch, bis die zweite Gleichung dem SOLL-Wert entspricht unter der Nebenbedingung, dass bei der ersten Gleichung der IST-Wert dem SOLL-Wert entspricht.
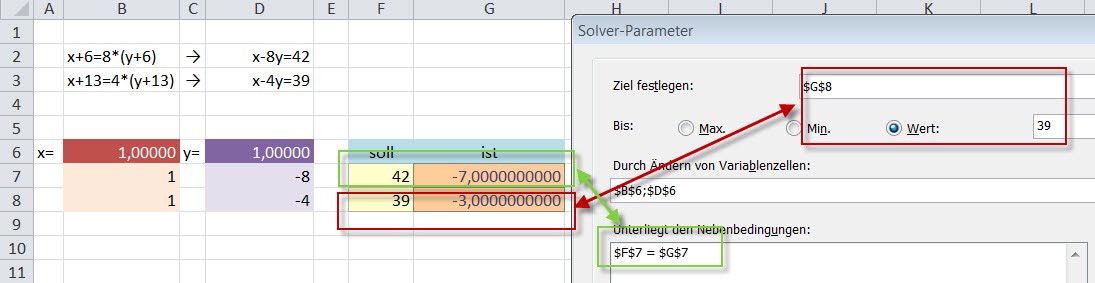
- Möglichkeit 3: Als dritte Möglichkeit legt man einen der IST-Werte mit Ziel MAXIMUM oder MINIMUM fest unter den Nebenbedingungen, dass bei beiden Gleichungen der SOLL-Wert dem IST-Wert entspricht.
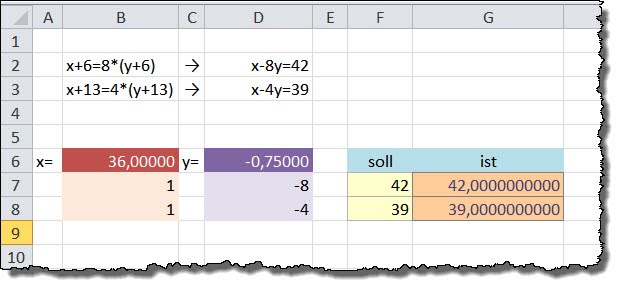
Egal welche der Methoden Sie anwenden Ergebnis ist immer das gleiche:
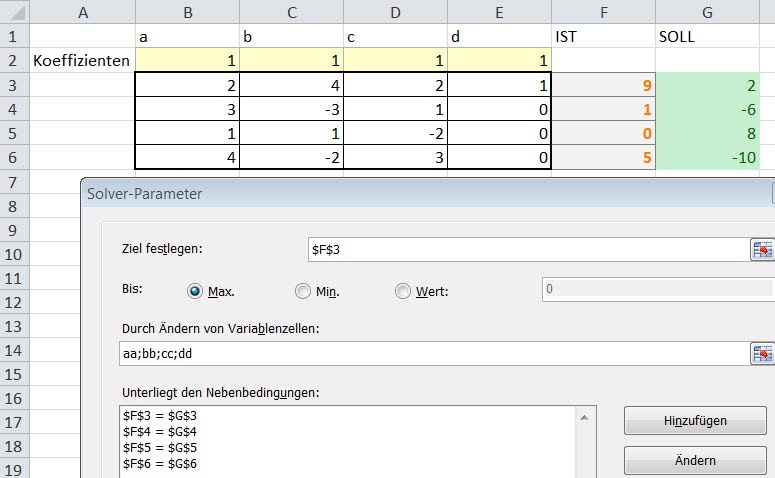
Beispiel 2: lineare Gleichungssystem mit 4 Unbekannten
Ein solches Gleichungssystem hätte man natürlich auch recht einfach per Hand lösen können. Bei mehr als 2 Gleichungssystemen ist das aber mit der Hand weitaus schwieriger. Daher das ganze nochmals mit 4 Gleichungssystemen mit 4 Unbekannten:
- I: 2a + 4b + 2c + d = 2
- II: 3a – 3b + c = -6
- III: a + b – 2c = 8
- IV: 4a – 2b + 3c = -10
Das mit der Hand zu lösen ist nicht ganz so einfach, aber in Excel stellt das kein wirkliches Problem dar.
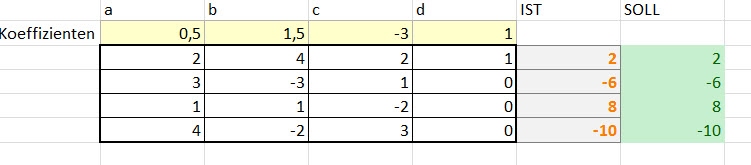
Wie man sieht ist es recht einfach auch Gleichungssystemen mit mehreren Unbekannten in Excel zu lösen.
Beispiel 3: nichtlineare Gleichungssystem
Es gibt aber noch weitere Vorteile dieser Methode zum Lösen von Gleichungssystemen: Es ist einerseits nicht zwingend notwendig, dass die Gleichungen in dieser Schreibweise erfolgen. dh. Es müssen nicht zwingend die Gleichungen umgeformt werden. Ein weiterer Vorteil ist dass es sich nicht zwingend um lineare Gleichungssysteme handeln muss. Anmerkung: Der Excel Solver wird nur eine Lösung finden, auch wenn es mehrere gibt.
Beispiel:
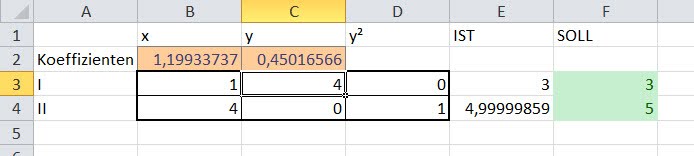
- x+4*y=3
- 4*x+y²=5
Per Hand würde man die Gleichungen nach x Auflösen und Gleichsetzen.
Mit Excel könnte man es folgendermaßen lösen:
und die Lösung
Lösen lineare Gleichungssysteme in Excel mittels Koeffizientenmatrix
Für einen Sonderfall von Matrizen gibt es jedoch noch eine andere sehr schnelle Lösung von Gleichungssystemen in Excel.
Aufgabenstellung:
- x+2y+z=6,50
- y+2z=5,2
- 3x+2y+z=9,50
Theorie
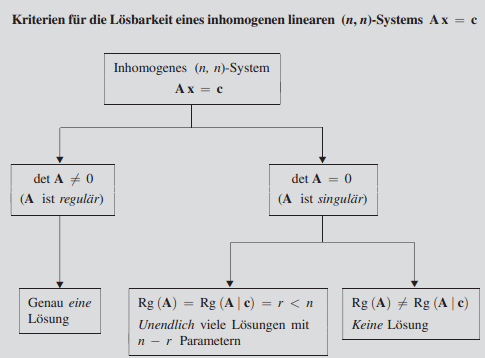
Für die Lösung solcher Gleichungssysteme in Excel müssen aber ein paar Kriterien erfüllt sein.
- Es muss sich um quadratische lineare Gleichungssysteme mit n Gleichungen und n Unbekannten handeln.
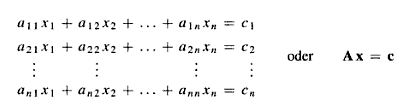
Die Koeffizientenmatrix A ist dabei quadratisch (n-reihig), die erweiterte Koeffizientenmatrix (A|c) vom Typ (n, n+1)
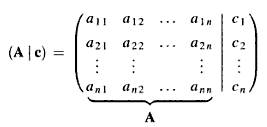
- Ein lineares quadratisches Gleichungssystem hat genau eine Lösung, wenn es sich um eine reguläre Matrix handelt. Dies ist für Matrizen der Fall, bei denen gilt:
 . Ist die Koeffizientenmatrix hingegen singuär (dh. det(A)=0), dann erhalten wir entweder unendlich viele Lösungen oder keine Lösung (mehr dazu im angehängten Dokument). Grundsätzlich ist es egal, ob es sich um inhomogene oder homogene quadratische lineare Gleichungssysteme handelt, für homogene gibt es jedoch noch eine weitere Einschränkung.
. Ist die Koeffizientenmatrix hingegen singuär (dh. det(A)=0), dann erhalten wir entweder unendlich viele Lösungen oder keine Lösung (mehr dazu im angehängten Dokument). Grundsätzlich ist es egal, ob es sich um inhomogene oder homogene quadratische lineare Gleichungssysteme handelt, für homogene gibt es jedoch noch eine weitere Einschränkung.
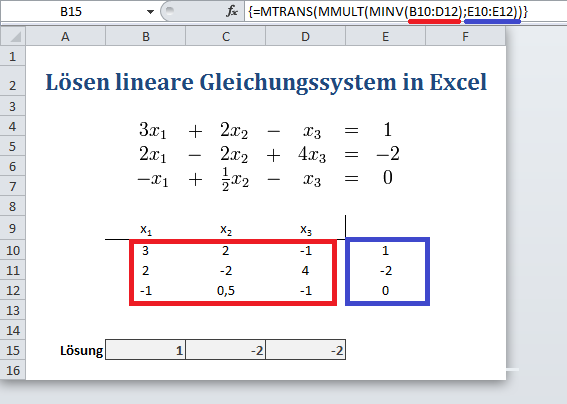
Das lineare Gleichungssystem mit drei Gleichungen und drei Unbekannten entspricht folgender Matrixgleichung:
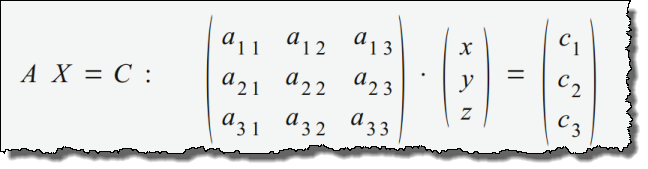
Für das konkrete Beispiel würde das bedeuten:
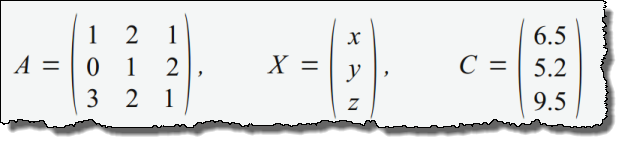
Nach einigen Umformungen ergibt sich folgendes
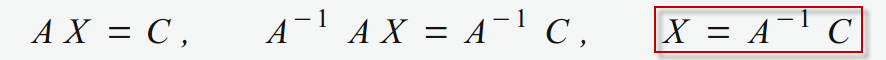
Lösung in Excel
Genug zu Theorie – Wie wirkt sich das nun auf die Anwendung in Excel aus.
- Man schreibe die Koeffizienten und deren Ausprägung in eine Excel Tabelle.
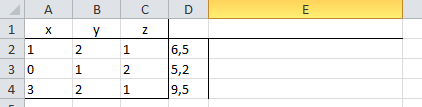
- in die Spalte daneben schreibt man nun die Matrixformel {=MMULT(MINV(Koeffizienten);Ergebnisse)}
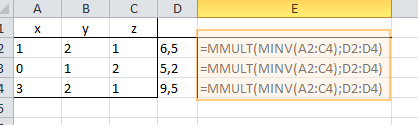
- und man erhält das Ergebnis
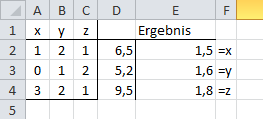
- Da diese Darstellung aber für den einen oder anderen verwirrend ist, kann man sich die Ergebnisse für die Koeffizienten unter der Matrix darstellen lassen. Hierfür muss das Ergebnis bzw. die Formel nur noch transponiert werden.
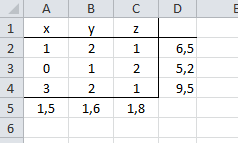

Zusammenfassung
Kurzzusammenfassung der Koeffizientenmatrix-Methode
Fazit
Beim Lösung von Gleichungssystemen gibt es in Excel 2 Möglichkeiten. Einerseits das Lösung mittels Excel Solver oder mittels Matrix. Der Solver hat den Vorteil, dass er nicht nur auf lineare Gleichungssystem begrenzt ist, sondern auch alle anderen Arten von Gleichungen lösen kann. Er hat jedoch den Nachteil, dass er nur eine mögliche Lösung findet und nicht alle möglichen Lösungen. Die Matrix-Methode hingegen ist auf lineare Gleichungen begrenzt, liefet jedoch immer alle Lösungen.
Daraus würde ich folgende Vorgehensweise ableiten:
- wenn es sich um eine lineare Gleichung handelt => Matrix-Methode
- wenn es sich nicht um eine lineare Gleichung handelt => Solver & grafische Darstellung, um herauszufinden, ob es mehrere Lösungen gibt.
weiterführende Informationen
Links:
Literatur:
- Papula, Lothar – Mathematik für Ingenierue und Naturwissenschaftler 2, S 83-90
Downloads

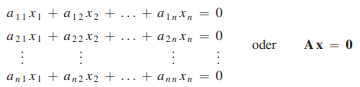



Comments
Richard Peters
Hallo Herr Erhard,
vielen Dank für die anschaulichen Darstellungen. Ich habe zwei kurze Fragen zu ihren Erläuterungen:
1. Ich wollte ihre Lösung mittels Koeffizientenmatrix nachbasteln, erhalte dabei jedoch in allen 3 Zellen das gleiche Ergebnis, das Sie für die erste Zelle angeben (1,5). Da scheint etwas mit der Darstellung der Funktion mmult nicht zu stimmen!?
2. Wieso muss ich Transponieren, wenn in den Formeln doch fixe Zellbezüge eingestellt sind? An diesen ändert sich doch nichts, auch wenn ich das Ergebnis in eine andere Zelle schreiben lasse.
Gruß
Richard Peters
Richard Peters
… Ergänzung: Ich glaube ich habs: Ich verwende Excel 2013. Dort muss man bei Array-Funktionen zum einen ALLE Zellen, in denen Berechnungen erstellt werden sollen, gleichzeitig markieren vor Eingabe der Funktion, und zum anderen die Eingabe mit Shift+Strg+Enter abschließen, nicht mit einfachem Enter. das war mir nicht bewußt. Bei Office365 fließt der Ergebisnisbereich automatisch in die nächsten Zellen und es reicht die einfache Enter-Taste (s. https://support.microsoft.com/de-de/office/minv-funktion-11f55086-adde-4c9f-8eb9-59da2d72efc6)
Gruß
Richard Peters