im 2-dimensionalen Raum (Satz des Pythagoras)
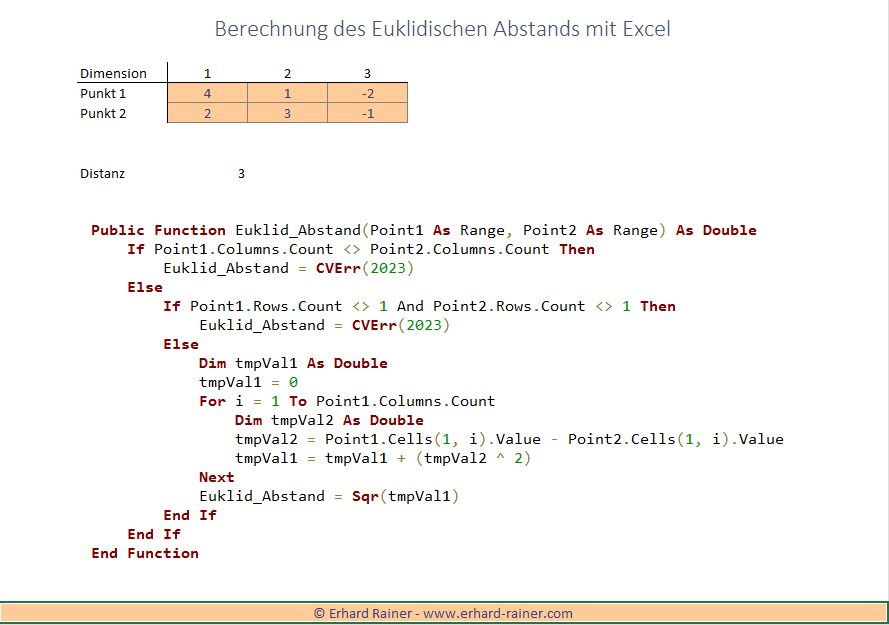
Um die Distanz zwischen zwei Punkten im zweidimensionalen Raum zu berechnen, kann man die Formel des Satzes des Pythagoras verwenden.
Um die Distanz zwischen zwei Punkten zu berechnen, ziehen Sie zunächst die x- und y-Koordinaten des einen Punkts von den x- und y-Koordinaten des anderen Punkts ab, um die Längen der Seiten des rechtwinkligen Dreiecks zu erhalten. Dann können Sie die Formel anwenden, um die Distanz zwischen den beiden Punkten zu berechnen.
Beispiel:
Angenommen, wir wollen die Distanz zwischen den Punkten (3, 4) und (0, 0) berechnen. In diesem Fall sind a = 3 und b = 4, also lautet die Formel:
c = √(3^2 + 4^2) = √(9 + 16) = √25 = 5
Der Satz des Pythagoras ist ein mathematischer Satz, der besagt, dass in einem rechtwinkligen Dreieck die Summe der Quadrate der Längen der beiden Katheten (die Seiten, die den rechten Winkel bilden) gleich der Quadratlänge der Hypotenuse (die Seite, die gegenüber dem rechten Winkel liegt) ist. Formal ausgedrückt lautet der Satz:
In einem rechtwinkligen Dreieck gilt: a^2 + b^2 = c^2
wobei a und b die Längen der Katheten und c die Länge der Hypotenuse sind. Dieser Satz ist eine der Grundlagen der Geometrie und wird häufig verwendet, um die Länge von Seiten in rechtwinkligen Dreiecken zu berechnen.
im n-dimensionalen Raum (Euklidischer Abstand)
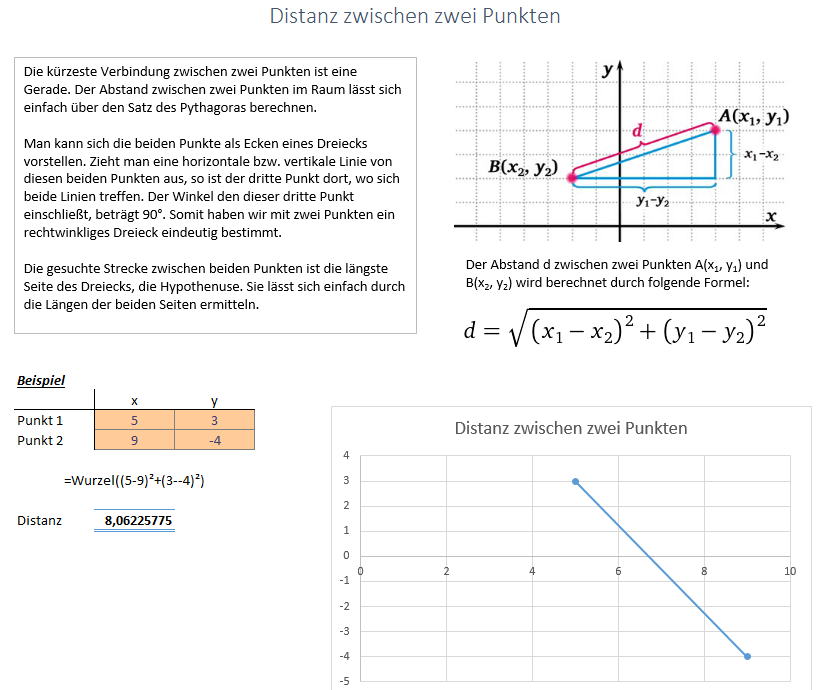
Um die Distanz zwischen zwei Punkten im dreidimensionalen Raum zu berechnen, kann man die Formel des Satzes des Pythagoras erweitern. Die Formel lautet in diesem Fall:
c = √(a^2 + b^2 + c^2)
wobei a, b und c die Längen der drei Seiten des rechtwinkligen Körpers sind, der die beiden Punkte umgibt, und c die Länge der Hypotenuse (also die gesuchte Distanz) ist.
Um die Distanz zwischen zwei Punkten zu berechnen, ziehen Sie zunächst die x-, y- und z-Koordinaten des einen Punkts von den x-, y- und z-Koordinaten des anderen Punkts ab, um die Längen der Seiten des rechtwinkligen Körpers zu erhalten. Dann können Sie die Formel anwenden, um die Distanz zwischen den beiden Punkten zu berechnen.
Beispiel:
Angenommen, wir wollen die Distanz zwischen den Punkten (3, 4, 5) und (0, 0, 0) berechnen. In diesem Fall sind a = 3, b = 4 und c = 5, also lautet die Formel:
d = √(3^2 + 4^2 + 5^2) = √(9 + 16 + 25) = √50 = 7,07
Zusammenfassung
Der Abstand zwischen zwei Punkten lässt sich über den Euklidischen Abstand ermitteln. Eine Sonderform dieses Abstands stellt der Satz des Pythagoras dar.
Man kann also den Abstand zwischen zwei Punkten auf folgende Arten erklären:
(1) Mit der Euklidischen Abstand-Formel (bzw. als Erweiterung des Satzes des Pythagoras)
(2) Als Betrag/Länge des Vektors zwischen zwei Punkten.
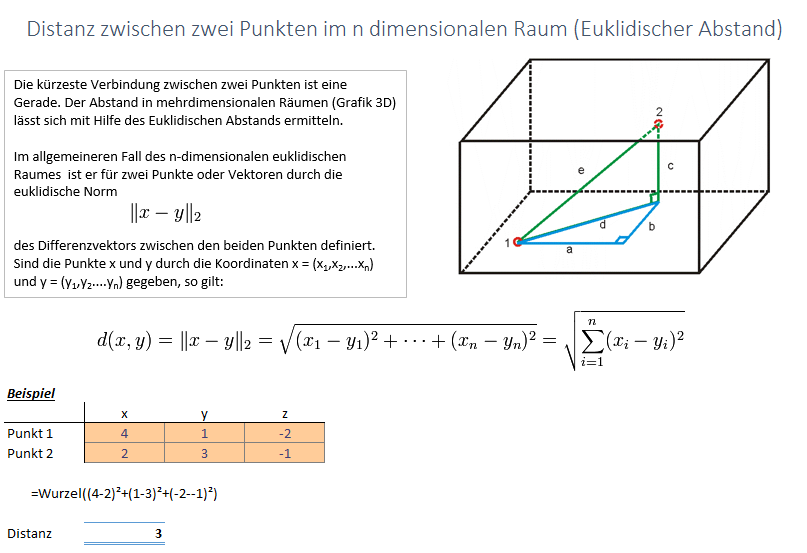
Berechnung in Excel
Grundsätzlich ist das in Excel sehr schnell berechnet, wie angehängte Tabelle zeigt, sofern man die Formel kennt.
Gerade im n-dimensionalen Raum kann das aber eine ganz schöne Tipperei sein. Mit folgender Funktion braucht man nur die Bereiche auswählen und bekommt den Euklidischen Abstand.