FINANZMATHEMATIK

Theoretische Grundlagen

Risikomanagement

Kapitalmarkttheorie / CAPM

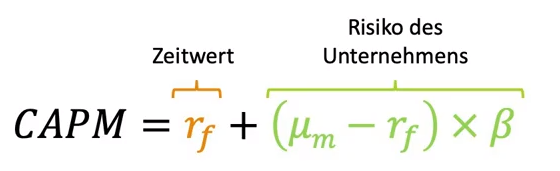
Kapitalmarkttheorie / CAPM (= Capital Asset Pricing Model) ist ein theoretisches Modell mit dem Wertpapiere bewertet werden können und es besagt, dass sich Anleger höhere Renditen durch hohes Risiko erkaufen müssen. Es handelt sich um eine Weiterentwicklung der Portfoliotheorie, die auch noch besagt, dass durch Diversifikation (Streuung) der Anlagen das effektive Risiko minimiert werden kann.

Effizienzmarkthypothese / Markteffizienzhypothese

Effizienzmarkthypothese (Efficient Market Hypothesis) besagt, dass Finanzmärkte effizient sind, insofern Informationen bereits eingepreist sind und somit keine Marktteilnehmer in der Lage sind durch technische Analyse, Fundamentalanalyse oder anderwertig dauerhaft überdurchschnittliche Gewinne zu erzielen. 

„A market in which prices always ‘fully reflect’ all available information is called ‘efficient’.”

“Nach Fama (1976, S. 134-137) lässt sich in einem effizienten Markt die Realität exakt durch alle verfügbaren Informationen wiedergeben. So werden nicht nur aktuelle und vergangene Daten wie Umsatzzahlen, BIP, politisches Klima, Präferenzen der Konsumenten und Investoren berücksichtigt, sondern auch die Interdependenzen und Kausalitätenzwischen den Daten. In einem effizienten Markt werden nicht nur aktuelle und historische Daten berücksichtigt, sondern auch Entwicklungen antizipiert. Die Akteure an den Märkten kennen nicht nur die Daten, sondern auch die zugehörigen datengenerierenden Prozesse. Treffen neue Informationen ein, nehmen die Marktteilnehmer eine Neubewertung der Unternehmenswerte vor und passen ihr Verhalten an, wodurch sich neue Preise ergeben. Einen Neuheitsgehalt haben Informationen nur, sofern sie nicht schon von den Akteuren antizipiert wurden. Einen Neuigkeitswert haben folglich nur Schocks, die entweder unmittelbar das Anlageverhalten beeinflussen oder die datengenerierenden Prozesse verändern und so mittelbar auf die Preise wirken.” [1]

Literatur:

• Fama, Eugene F. – Effizient Capital Markets: A Review of Theory and Empirical Work (1970) [Quelle]

Quellen:[1] Will, Matthias Georg – Eine kurze Ideengeschichte der Kapitalmarkttheorie: Fundamentalanylse, Effizienzmarkthypothese und Behavioral Finance. [Diskussionspapier 2012-04]

Grundlagen

Zinsrechnung

Die Zinsrechnung beschreibt ein mathematisches Verfahren zur Berechnung von Zinsen, die als Entgelt auf geliehene Geldbeträge erhoben werden.
Grundsätzlich unterteilt sich die Zinsrechnung in die 

• „Einfache Zinsrechnung“ (lineare Verzinsung), bei der anfallende und nicht ausgezahlte Zinsen sowie der zu verzinsende Geldbetrag, z. B. Kredit, Darlehen oder Spareinlage, nicht addiert werden, und 
• die Zinseszinsrechnung, bei der nicht ausgezahlte Zinsen zum Grundbetrag addiert und bei der weiteren Verzinsung berücksichtigt werden.

Links:

• Schiffers, Anja – einfache Zinsrechnung (für Anfänger!)
• einfache Zinsrechnung (online Berechnung)

Rentenrechnung

Tilgungsrechnung

Tilgungsrechnung befasst sich mit der systematischen Rückzahlung von Schulden oder Darlehen über einen festgelegten Zeitraum hinweg. Sie legt fest, wie und in welchen Raten ein geliehener Betrag inklusive Zinsen an den Gläubiger zurückgezahlt wird.

Finanzinstrumente

Wertpapier Basics (Youtube Serie)

Grundlagen

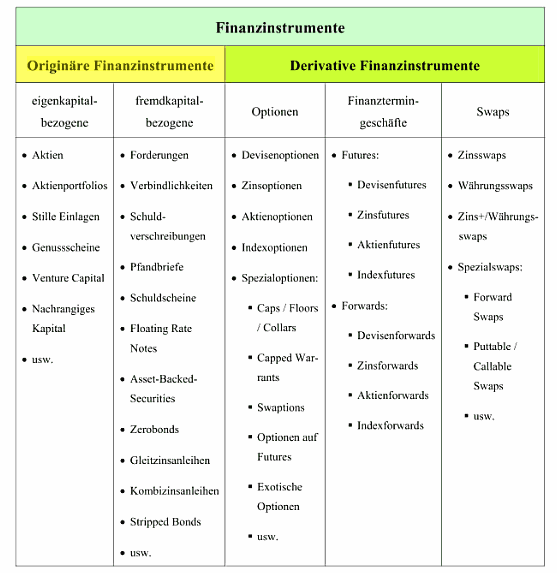
Unter einem Finanzinstrument sind alle vertraglichen Ansprüche und Verpflichtungen zu verstehen, die unmittelbar oder mittelbar den Austausch von Zahlungsmitteln zum Gegenstand haben. Die aus Verträgen oder Vereinbarungen resultierenden Rechte bzw. Pflichten müssen dabei auf finanziellen Sachverhalten beruhen. [Wikipedia]

• Originäre Finanzinstrumente verkörpern Fest- oder Residualansprüche, die auf die unkonditionale Leistung von Geldbeträgen gerichtet sind. Sie lassen sich in eigenkapital- und fremdkapitalbezogene Finanzinstrumente untergliedern.
  • Unter eigenkapitalbezogenen Finanzinstrumenten versteht man bspw Aktien, stille Einlagen, Genussscheine sowie Venture Capital.
  • Fremdkapitalbezogene originäre Finanzinstrumente sind zB Forderungen, Verbindlichkeiten und Schuldscheine.
• Derivative Finanzinstrumente (kurz: Derivate) sind Finanzinstrumente, deren Wert aus einem zugrundliegenden Bezugsobjekt (sog. Underlying) abgeleitet wird. Häufig kommen als zugrundliegende Basiswerte originäre Finanzinstrumente, wie etwa Aktien oder Schuldverschreibungen, aber auch Aktienindizes oder Gütergeschäfte in Betracht. Die gängigsten Grundformen derivativer Finanzinstrumente sind Optionen, Forwards und Futures.
  • Sonderform: eingebettete Derivate: Des Weiteren können Kombinationen verschiedener Derivate und modifizierter originärer Finanzinstrumente (Trägerinstrumente bzw. Basisvertrag) als derivative Finanzinstrumente verstanden werden. Ein klassisches Beispiel für eingebettete Derivate stellen die Wandelschuldverschreibungen dar. Hier hat der Gläubiger der Wandelschuldverschreibung neben Zins- und Tilgungsanspruch aus der Anleihe (=Trägerinstrument) zusätzlich das Recht, die Anleihe innerhalb einer bestimmten Wandlungsfrist in einem vorher festgelegten Wandlungsverhältnis in Aktien der emittierenden Gesellschaft umzutauschen. Wichtig für die Abgrenzung als eingebettete Derivate ist, dass die beiden Komponenten (Trägerinstrument und eingebettetes Derivat) aus rechtlicher Sicht nicht trennbar sind und deshalb auch nicht seperat veräußert werden können. So sind zB die Optionsrechte in den Optionsschuldverschreibungen keine eingebetteten Derivate, da sie separat im Mark veräußert werden können.

Sparquote

Mit Sparquote bezeichnet man in der Volkswirtschaftslehre den Anteil der Ersparnisse am Einkommen. Unterschieden wird dabei:

• Durchschnittliche Sparquote der privaten Haushalte, die als der Anteil der Ersparnisse am verfügbaren Einkommen definiert ist.
• Gesamtwirtschaftliche Sparquote, die das Verhältnis der Ersparnisse der gesamten Volkswirtschaft (der Haushalte, der Unternehmen und des Staates) in Relation zum Bruttoinlandsprodukt angibt.
• Marginale Sparquote, die die Veränderung der Ersparnisse bei einer Einkommensänderung angibt. Dabei liegt die Sparquote zwischen 0 und 1.

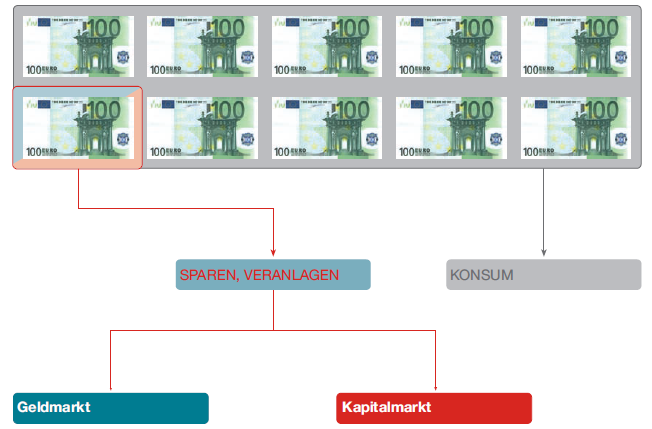
orginäre / traditionelle Finanzinstrumente (primary financial instruments)

• gekennzeichnet durch den Abschluss von Kassageschäften (dh. Vertragsabschluss und Erfüllung fallen zeitlich zusammen)
• Beispiele:
  • festverzinslicher Wertpapiere
  • Aktien

derivate Finanzinstrumente (derivative financial instruments)

•  Derivate (Swaps, Optionen) – leiten sich von den zugrundeliegenden originären Finanzinstrumenten (sog. Basiswert (underlying)) ab. Weiters sind sie gekennzeichnet dadurch, dass keine oder nur eine vergleichsweise geringe Anfangsinvestition erforderlich ist sie in Zukunft abgewickelt bwz. 
• Futures / Forwards
• Optionen
• Forward-Rate-Agreement –  Spot Rates | Forward Rates
• Caps, Floors, Collars
• Swaps

Geldmarktinstrumente

• Konditionen für Sparbücher – Vergleich – www.bankkonditionen.at 
• Inflation Österreich (aber auch andere Länder)

Risikokennzahlen

Eine Investition  ist immer auch mit einem gewissen Risiko verbunden, denn je höher die Renditechancen, desto höher das Risiko. Jeder Anleger muss daher entscheiden, welche Rendite er anstrebt und wie viel Risiko er dafür in Kauf nehmen will.

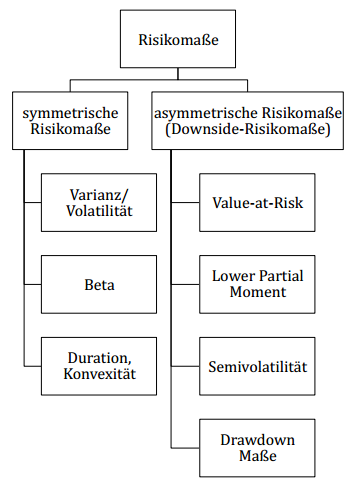
Value-at-Risk

• Definition
  • angibt, welchen Wert der Verlust einer bestimmten Risikoposition (z. B. eines Portfolios von Wertpapieren) mit einer gegebenen Wahrscheinlichkeit innerhalb eines gegebenen Zeithorizonts nicht überschreitet. – dh.
    • es ist der Versuch das Ausmaß künftiger Verluste abzuschätzen
    • VaR ist der erwartete max. Verlust, der mit einer festgelegten Wahrscheinlichkeit nicht überschritten wird. 
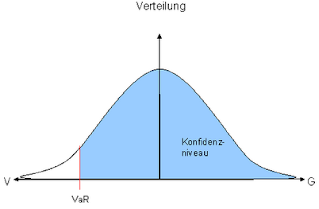
    • Ausgehend von fixierten Zeitintervall und vorgegebener Ausfallwahrscheinlichkeit (Konfidenzniveau) ist der VaR die Verlusthöhe, die mit der vorgegebenen Wahrscheinlichkeit nicht überschritten wird (Probable Maximum Loss).
  • Wikipedia | FinanceWiki
  • Beispiel

Link

• Webseiten:
  • DJE – Risikokennzahlen
• Artikel/Dokumente
  • Hößl, Wolfgang – Methoden der Risikomessung und ihre Aussagekraft für Investoren
  • Bürkler, Nikolaus – Rendite, Risiko, Performance – eine Übersicht
  • Börsenzeitung – Asymmetrische Risikomaße finden immer häufiger Anwendung (13.11.2010)
  • Gütlbauer, Karin – Rendite-, Risiko- und Performancemaße für Investments
  • Pichler, Stefan – Risk Management
• Bücher
  • Fischer, Bernd R. – Performanceanalyse in der Praxis, S 389-449 [GoogleBooks | Amazon]
  • Diederichs, Marc – Risikomanagement und Risikocontrolling [GoogleBooks | Amazon]
  • Christians, Uwe – Performance Management und Risiko [GoogleBooks | Amazon]
  • König, Alexander – Ansätze zur Risikoanalyse und Risikobewältigung in der Lebensversicherung [GoogleBooks | Amazon]

Finanzmathematik & Excel

Sonstiges

• Zertifizierung:
  • Börse Wien: Lehrgang: Börsenhändler – Kassamarkt | Diplomprüfung Kassamarkt
  • Börse Fankfurt: Zertifizierter Börsenhändler Kassamarkt

Literatur

• Pfeifer, Andreas – Praktische Finanzmathematik: Mit Futures, Optionen, Swaps und anderen Derivaten [GoogleBooks | Amazon]
• Pfeifer, Andreas – Finanzmathematik (Übungsbuch mit Formelsammlung) [GoogleBooks | Amazon]
• Luderer, Bernd – Mathematische Formeln für Wirtschaftswissenschaftler [GoogleBooks | Amazon]
• Peters, Horst – Wirtschaftsmathematik (Lehrbuch) [GoogleBooks | Amazon]
• Tietze, Jürgen – Einführung in die Finanzmathematik [GoogleBooks | Amazon]
• Renger, Klaus – Finanzmathematik mit Excel [GoogleBooks | Amazon]
• Luderer, Bernd – Mathematische Formeln für Wirtschaftswissenschaftler [GoogleBooks | Amazon]
• Luderer, Bernd – Arbeits- und Übungsbuch zur Wirtschaftsmathematik [GoogleBooks | Amazon]
• Grundmann, Wolfgang – Formelsammlung Finanzmathematik, Versicherungsmathematik, Wertpapieranalyse [GoogleBooks | Amazon]