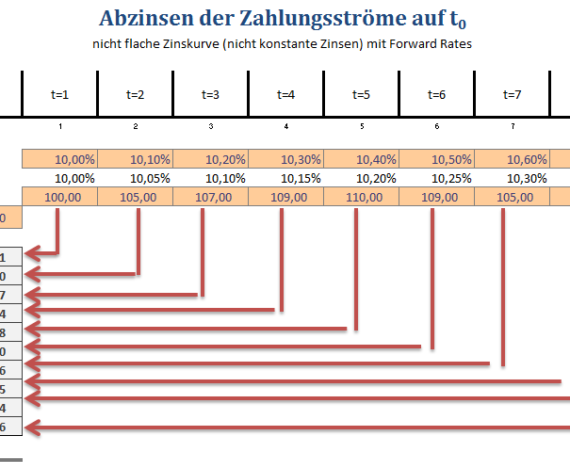
In der Investitionsrechnung hat man oftmals mit langen Zahlungsreihen zu tun, deren Kapitalwertberechnng eine ziemliche Tipperei ist, die darüberhinaus noch sehr fehleranfällig ist. In der Praxis werden daher meist eingebaute Funktionen zur Berechnung verwendet. In Excel sind beispielsweise alle grundlegenden Funktionen eingebaut. Für den TI-Taschenrechner habe ich die Basisfunktion nachprogrammiert.
periodische Cash-Flows
Kapitalwert (Excel, TI-Basic)
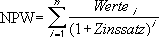
Berechnung des Kapitalwertes mittels Excel (NPV/NBW)
Excel stellt für die Kapitalwertberechnung eine Funktion zur Verfügung:
Diese berücksichtigen jedoch nur die CF für t>0 (also nicht die Anfangsinvestition), wodurch die Anfangsinvestition (zum Zeitpunkt t=0) zusätzlich abgezogen werden muss. Diese Investition muss auch nicht abgezinst werden.
Beispiel:
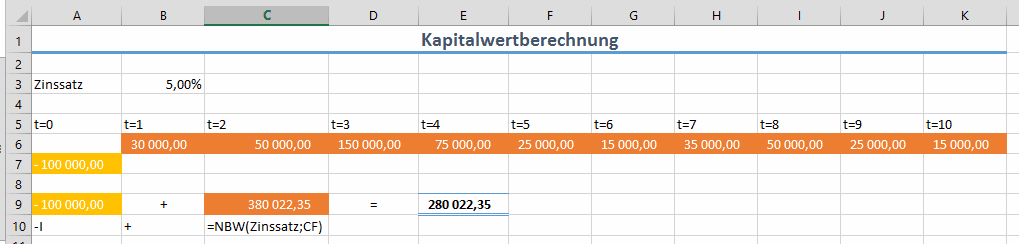
schrittweise Vorgehensweise:
- Die CF für t>0 (t=1,2,3,…n) [Anmerkung: in diesem Beispiel orange – horizontal)
- Die Anfangsinvestition mit negativen Vorzeichen niederschreiben (ich schreibe es idR vor dem ersten CF und ordnet den Wert der Periode t=0 zu; das negative Vorzeichen ergibt sich daraus, dass es sich bei der Anfangsinvestition um einen negativen CF handelt)
- Berechnung := Anfangsinvestition + NBW(Zinssatz;CF)
Wenn man zwischen Haben- und Sollzinssätze unterscheiden soll, dann kann man auf die modifizierte Nettobarwert-Formel zurückgreifen.
Die NPV-Funktion in TI-Basic nachgebildet
TI-Basic:Die meisten (ich kenne jedenfalls keinen) Taschenrechner von TI stellen kein Pendant für die Kapitalwertberechnung zur Verfügung. Aus diesem Grund habe ich die Kapitalwertfunktion in TI-Basic nachgebaut. Die Schreibweise der Formel erfolgt in Anlehnung an die Schreibweise in Excel (NPV)
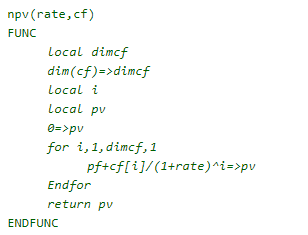
Beispiel: Eine Investition von 100.000 führt zu CFs für die Jahre t=1 bis t=10 und der Zinssatz von 5%: {30.000,50.000,150.000,75,000,25,000,15.000,35.000,50.000,25.000,15.000}
Eingabe am TR: -100000 + npv(0.05,{30000,50000,150000,75000,25000,15000,35000,50000,25000,15000}) = 280022,35
weiterführende Literatur:
Interner Zinssatz
Berechnung des internen Zinsfusses in Excel (Zielwertsuche, IKV/IRR)
Der interne Zinssatz ist definiert, dass man den Kapitalwert null gesetzt wird (NPV=0) und der Zinsfuß (Zinssatz) gesucht wird, damit die Gleichung stimmt. dh. Der interne Zinsfuss ist genau der Zinssatz, der bei Verwendung als Kalkulationszins zuin der Kapitalwertmethode zu einem Kapitalwert von 0 führt.
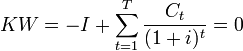
In Excel gibt es für dieses Problem zwei Herangehensweisen:(a) mittels Zielwertsuche(b) mittels spezieller Excel Formel:
Der IKV (interne Zinsfuß) geht von regelmäßigen Cashflows aus. Was aber wenn diese unregelmäßig sind? => XINTZINSFUSS (siehe unten)
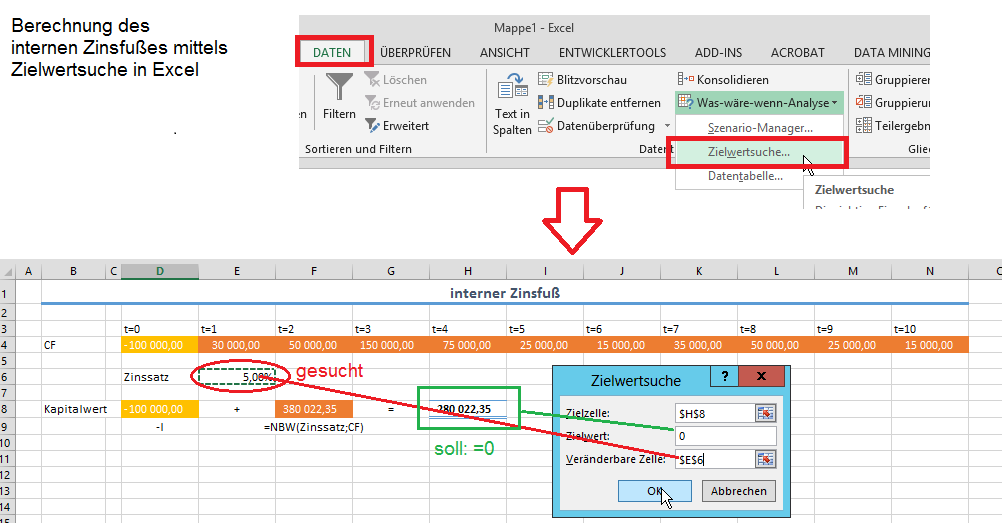
Beispiel: Möchte man den internen Zinsfuß für oben erwähntes Beispiel mittels Zielwertsuche berechnen, geht man folgendermaßen vor:
- Eingabe analog zu oben
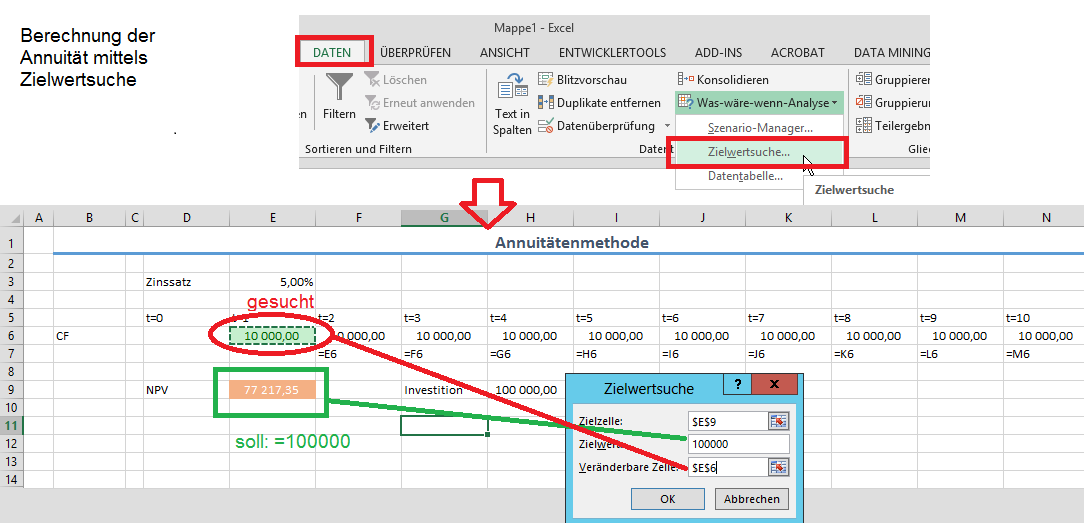
- Aufrufen der Zielwertsuche: Daten > was wäre wenn Analyse > Zielwertsuche
- Eingabe Zielwertsuche:
- Zielzelle: Kapitalwert
- Zielwert: 0
- veränderbare Zelle: Zinssatz
Berechnung mittels IKV/IRR

IKV in TI-Basic nachgebildet
TI-Basic:Nicht identisch mit der Excel-Funktion ist die Schreibweise der Funktion für TI-Rechner. Dafür ist das Ergebnis genauer:

Für das Beispiel bedeutet dies folgende Schreibweise
ikv({30000,50000,150000,75000,25000,15000,35000,50000,25000,15000},100000} = 0,556157126512 = 55,6157126512%
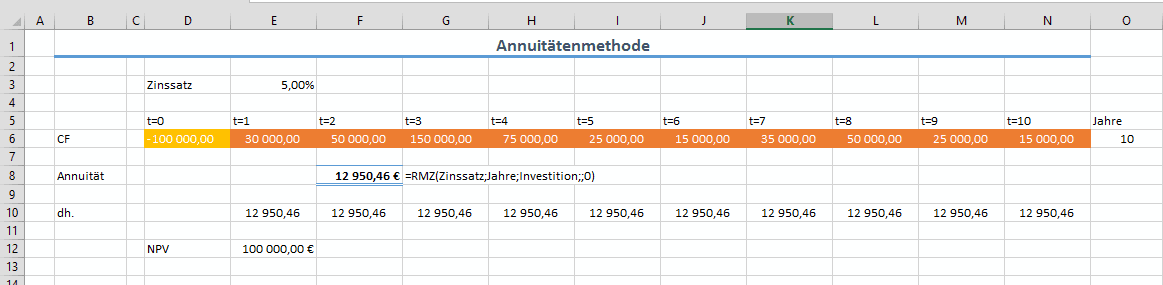
Annuitätenmethode
Hinter der Annuitätenmethode steckt die Frage, wie hoch die CFs über die Laufzeit wären, wenn diese immer gleich hoch sind, um die Investitionssumme wieder zu lukrieren.
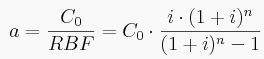
Berchnung der Annuitäten in Excel (RMZ/PMT)
In Excel gibt es dafür folgende Funktionen:
Die Annuitätenmethode kann man auch mit der Zielwertsuche berechnen:
Wozu aber diese Methode, wenn man doch mit RMZ einfacher zum Ziel kommt?
Hierzu folgendes Beispiel: Wie hoch sind die CFs, wenn der Kapitalwert 100.000 ist und die CF jedes Jahr um 10% steigen. (anders formuliert: Wie hoch können die Entnahmen sein, wenn sie jedes Jahr um 10% steigen und die Anfangsinvestition 100.000 ist. Der Zinssatz ist 5%)
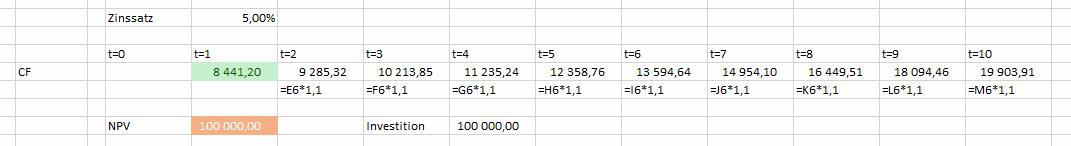
RMZ in TI-Basic nachgebildet
Für den TI-Rechner könnte man die Formel folgendermaßen nachbilden
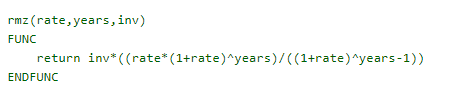
Für unser Beispiel bedeutet dies folgende SyntaxAnnuität:
rmz(0.05,10,100000) = 12950,46
unperiodische Cash-Flows
Kapitalwert bei unperiodisch anfallenden Zahlungen
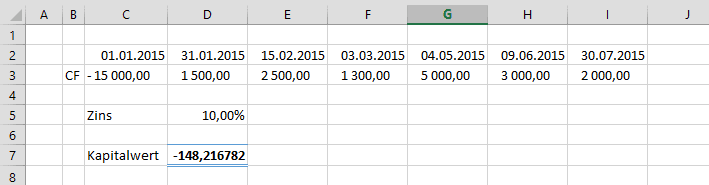
Kapitalwert bei unperiodisch anfallenden Zahlungen in Excel (XKAPITALWERT)
XKAPITALWERT gibt den Nettobarwert (Kapitalwert) einer Reihe nicht unbedingt periodisch anfallender Zahlungen zurück:

XKAPITALWERT(Zins; Werte; Daten)
interner Zinsfuß bei unperiodisch anfallenden Zahlungen
interner Zinsfuß bei unperiodisch anfallende Zahlungen in Excel (XINTZINSFUSS)
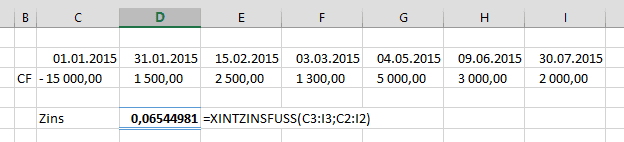
Aber was zum Teufel ist die XINTZINSFUSS()? [englisch: XIRR] – gibt den internen Zinsfuß einer Reihe nicht unbedingt periodisch anfallender Zahlungen zurück

XINTZINSFUSS(Werte; Daten; [Schätzwert])
Beispiel: Am 1.1.2015 wird ein Kreditaufgenommen, der mit folgenden Einzahlungen getilgt werden soll. Wie hoch darf der Kreditzinssatz sein, damit am Ende kein Guthaben und auch kein Minus am Konto ist?
Literatur:
- Jeschke, Egbert – Microsoft Excel: Formeln & Funktionen – Das Maxibuch (2. Auflage), S 704
Links
- für weitere finanzmathematische Funktionen in Excel siehe hier.
- Berechnung von Kapitalwerten und weitere Barwertfunktionen