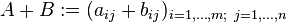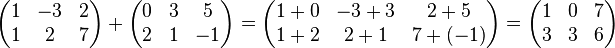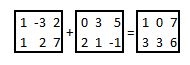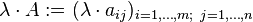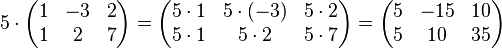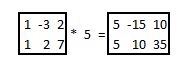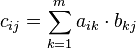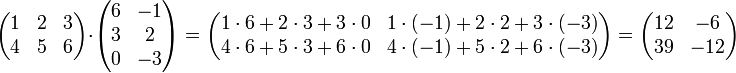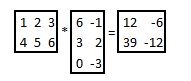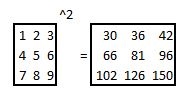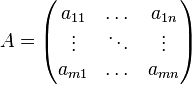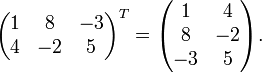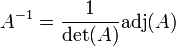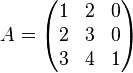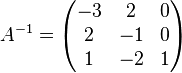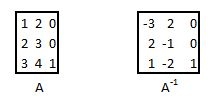Vorbemerkungen
Beim Rechnen mit Matizen in Excel sind zwei Eigentümlichkeiten zu beachten:
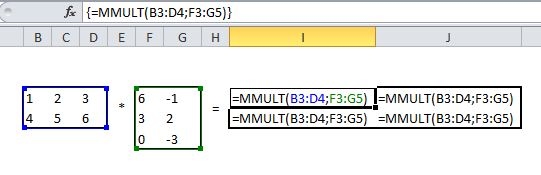
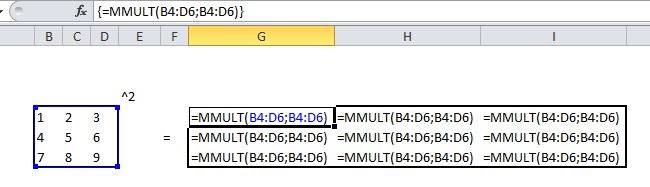
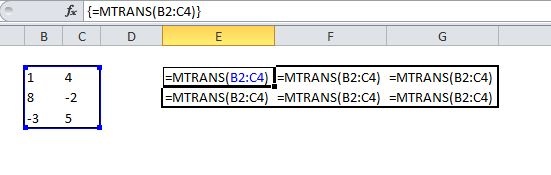
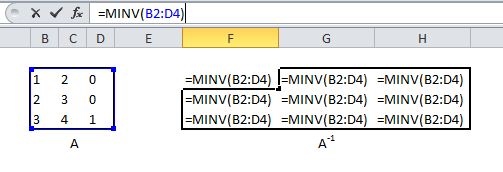
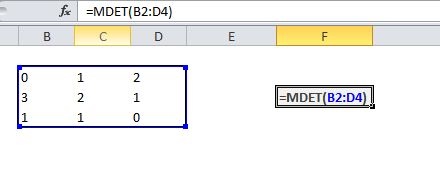
- Der Zielbereich der Operation, also die Zellen, in die die Ergebnisse der Operation eingefügt werden, müssen vor der Befehlseingabe (= …) komplett markiert werden. Erst danach wird in der Eingabezeile die Operation eingegeben.
- Das Bestätigen der in die Eingabezeile eingegebenen Operation erfolgt nicht wie gewohnt durch einfaches Drücken der Return-Taste, sondern durch das gleichzeitige Drücken von Strg+Shift+Return.
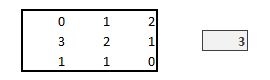
In der Eingabezeile sieht man, wie der entsprechende Befehl („=…“) in geschweifte Klammern {=…} gesetzt wird. Dies ist das Zeichen dafür, dass EXCEL den Eingabebefehl – korrekt – auf das gesamte markierte Feld bezieht.
Buchtipp
Wer sich mit der Thematik intensiver beschäftigen möchte, dem kann ich das Buch Benker, Hans – Wirtschaftsmathematik – Problemlösungen in Excel (Grundlagen, Vorgehensweisen, Aufgaben, Beispiele) [GoogleBooks | Amazon] sehr empfehlen.
Addition und Multiplikation
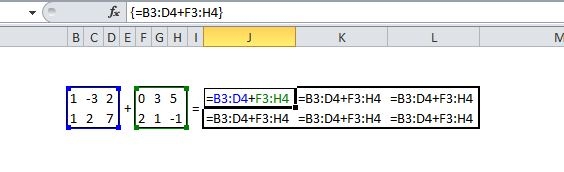
Matrizenaddition
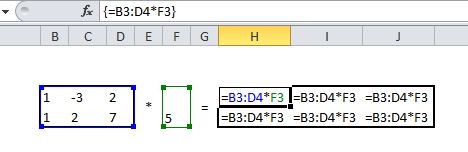
Skalarmultiplikation
Matrizenmultiplikation
Potenzieren von Matrizen
Quadratische Matrizen können auch potentiziert werden (siehe dazu hier)
weitere Rechenoperationen
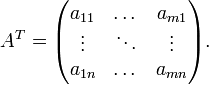
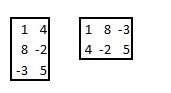
Transponieren einer Matrix (MTRANS)
MTRANS
Inverse Matrix (MINV)
Zu den mathematischen Grundlagen siehe hier.
Vektor-Vektor-Produkte (Skalarprodukt und Tensorprodukt)
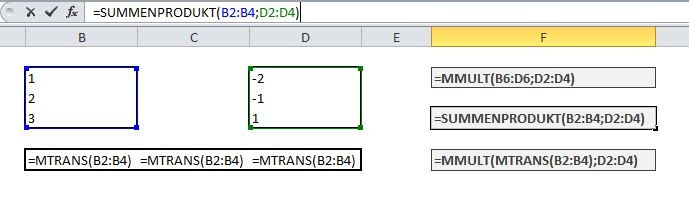
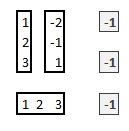
kanonisches Skalarprodukt
Das Skalarprodukt a⋅b ist eine Multiplikationsoperation für beliebige n-dimensionale Vektoren a und b und folgendermaßen charakterisiert: Es berechnet sich als Summe der Produkte entsprechender Komponenten beider Vektoren a und b, d.h.

hierzu gibt es 2 Methoden:
- {=MMULT(MTRANS(VektorA);VektorB)}
- =SUMMENPRODULT(VektorA;VektorB) – diese Methode bevorzuge ich persönlich
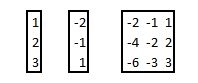
dyadisches Produkt / Tensorprodukt

Einheitsmatrix
Leider gibt es in Excel keine Funktion für eine Einheitsmatrix, daher empfiehlt sich folgende Vorgehensweise:
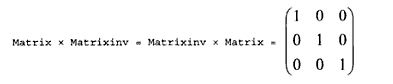
Rang einer MatrixFür diese Aufgabe habe ich in Excel leider noch keine Lösung gefunden. Wer eine Idee hat, kann sich gerne bei mir melden.