Ein Körper der Temperatur T0, die höher als die (konstante) Umgebungstemperatur U ist, kühlt sich durch Wärmestrahlung, Wärmeleitung und Konvektion ab. Dabei ist nach Newton die Temperaturänderung mit der Zeit dT/dt proportional zur Differenz der Temperatur T0 des Körpers und der Umgebungstemperatur U.
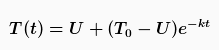
wobei k = Proportionalitätskonstante ist.
Dazu ein Beispiel: Eine Leiche mit einer Temperatur von 32° wird um 0:15 gefunden. Nach der Überstellung in die Gerichtsmedizin, die um 0:32 abgeschlossen ist, hat der Leichnam noch eine Temperatur von 29,93°. Wann genau ist der Mord geschehen, wenn die gesamte Nacht die Umgebungstemperatur konstant 15° C war? Dh. Innerhalb von 17 Minuten hat sich die Leiche um 2,07°C abgekühlt, bei einer konstanten Umgebungstemperatur von 15°C.
Daraus errechnet sich eine Proportionalitätskonstante (k) von = 0,007635689632154.
Geht man davon aus, dass die lebende Person eine Körpertemperatur von 37°C gehabt hat, ergibt sich folgender Todeszeitpunkt: 33,76 Minuten vor dem Auffinden der Leiche fand der Mord statt. Also um ca 23:41.
Beispiel 2: Peter hat für seine Party heute Abend Bier eingekauft, hat aber vergessen das Bier rechtzeitig einzukühlen. Jetzt 2h vor Partybeginn möchte er wissen, ob das Bier in seinem 7°C kalten Kühlschrank noch rechtzeitig auf angenehme 8″ abkühlen kann. Da er das Bier direkt vor einem sonnenbeschienen Fenster lagert, hat das Bier derzeit eine Temperatur von 16°C. Aus Erfahrung weiß er, dass ein 10°C warmes Bier für die Abkühlung auf 8°C genau 1,5h benötigt.
Auf Basis dieser Angabe kann man den Wert für k (Proportionalitätskonstante) errechnen. Diese beträgt für das Bier = 0,012206803207423.
Auf Basis dieses Wertes kann man jetzt die Zeit ermitteln, die das Bier von 16°C auf 8°C benötigen würde. Nach ca. 3h hätte das Bier die gewünschte Temperatur.
Da er aber nur mehr 2h Zeit für die Kühlung des Biers hat, wird das erste Bier, das er zu Party-Beginn ausschenkt nur eine Temperatur von 9,08° C haben.
Literatur:
- Kopie des Orginaldokuments
- Griull, U. – Newton’s temperature scale and the low of cooling (Wärme- und Stoffübertragung 18, 195-199 (1984))
- Griull, U. – Das Newtonsche Abkühlungsgesetz (Bemerkungen zu einer Arbeit von Isaac Newton aus dem Jahre 1701)
- Ruffner, J. – Reinterpretation of the Genesis of Newton’s „Law of Cooling“
- Besson, U. – The History of the Cooling Law – When the Search for Simplicity can be an Obstacle
- Besson, U. – Cooling and warming laws: an exact analytical solution
- Wärmeübertragungskoeffizient (Wikipedia)
- Thermodynamik – Wärmetransport
- Uni Graz USW – Das Newtonsche Abkühlungsgesetz
- Formelsammlung zu Wärme- und Stoffübertragung
- Herleitung Abkühlungsgesetz
- Bücher
- Burg, Klemens – Höhere Mathematik für Ingenieure, S 3
- Grigull, U. – Grundgesetze der Wärmeübertragung [GoogleBooks | Inhaltsverzeichnis | Springer]
- Herwig, Heinz – Wärmeübertragung
- Marek, Rudi – Praxis der Wärmeübertragung [GoogleBooks | Amazon]
- Mach, E. – Die Prinzipien der Wärmelehre
- Bernhard, Frank – Technische Temperaturmessung



